基于分子動力學方法研究金屬層合板軋制復合過程界面區材料的微觀變形行為,從力學性能和位錯運動的角度,對比研究雙金屬FeCrNi/Fe與單金屬的壓縮變形,揭示非共格界面對金屬微觀變形行為的影響。結果表明,雙金屬模型與2種單金屬模型在應力-應變關系和變形行為規律方面都存在明顯差異;由于復合界面的存在,變形過程中雙金屬模型純Fe基體中的位錯在界面附近積累,界面原子的局部剪切作用使FeCrNi基體中的位錯形成變得容易,降低了FeCrNi基體的屈服強度;復合界面對于變形過程中位錯傳播的阻礙作用,使材料抵抗塑性變形的能力得到提高,變形過程中2種金屬基體內位錯密度的交替變化導致2種金屬基體的變形量也對應呈現交替變化的特殊現象。
關鍵詞:
軋制復合是目前金屬層合板的主要制備方法,與爆炸焊等方法相比,具有復合質量高、生產效率高、安全便捷等優點[1,2,3]。軋制復合不銹鋼-碳鋼層合板時,上下軋輥旋轉并以表面摩擦力驅動分離狀態的各層金屬帶,依序快速完成復合的一系列連續工藝過程,包括各層金屬帶運動前進、被咬入輥縫、被軋制減薄乃至層間接觸界面實現結合后離開輥縫。其中,在軋制減薄過程中,各層鋼帶因軋制發生劇烈塑性變形,使金屬表面破裂,裸露出未氧化、無污染的新鮮本體材料,并在軋制壓力作用下界面兩側表層材料相互接近到原子尺度的接觸而產生兩側原子間鍵合以及原子跨界面擴散,從而實現不銹鋼與碳鋼的大面積固相復合。軋制減薄過程中基材的變形和接觸是實現復合的基礎工藝條件,界面原子的鍵合和擴散是實現復合的物理機制,實現界面間大面積類似冶金結合是復合的技術質量目標。軋制復合過程中各組元基材的變形協調性與其軋制工藝以及各基材的軋前初始厚度比和塑性本構有關,并嚴重影響復合質量與界面結合強度[4,5]。與擴散焊接和摩擦焊接軋制復合不同,軋制復合既有異種金屬間原子的鍵合與擴散現象,還伴隨著基材金屬的劇烈塑性變形。因此,研究不銹鋼與碳鋼軋制復合理論與技術,除了需要仿真或實驗研究復合變形過程中基材的彈塑性變形行為和實現復合的臨界工藝條件,還需圍繞界面層金屬原子的運動與位錯的演化,從微觀尺度上探索不銹鋼與碳鋼軋制復合過程塑性變形行為。
勢函數的選擇是分子動力學模擬中的關鍵問題。目前,針對具有相同晶格結構雙金屬復合過程的模擬,已提出多個適用的勢函數,模型及建模都較為成熟,并且已經針對fcc-fcc結構的Al-Fe、Cu-Fe、Fe-Ni和bcc-bcc結構的Cr-Fe等開展了相關研究,Mendelev等[11]開發了一種可以準確描述Al-Fe體擴散過程的勢函數,基于此分析了Al中Fe雜質對晶界遷移的影響;Bonny等[12]開發了一種三元多體Fe-Cu-Ni勢函數,并通過模擬退火實驗對勢函數進行了驗證;Stukowski等[13]提出了更有效計算Cr-Fe體系中單個粒子位移/變形能的EAM (embedded-atom method)勢函數。但是,針對具有不同晶格結構雙金屬復合過程的模擬,由于很難用一種勢函數同時準確描述2種或者更多種晶格結構的材料,導致目前的各個勢函數都不能獲得理想的模擬結果,其適用性尚難以評價比較。
在雙金屬或多金屬復合材料塑性變形過程中,界面有著重要的影響。界面既可以阻礙位錯運動,也是位錯的發射源[14,15,16]。近年來,國內外學者利用分子動力學方法,針對界面對多層金屬的塑性變形影響機理開展了廣泛的研究,Shao和Medyanik[17]模擬了非共格界面的Cu/Nb雙金屬在納米壓痕儀作用下位錯的增殖和演化行為,研究了不同加載過程中變形機理的差異;Wang等[18]用相似的方法進行了研究,認為在Cu/Nb非共格界面系統中界面會阻礙滑移位錯的發射;Misra等[19]同樣針對Cu/Nb雙金屬利用分子動力學方法進行變形模擬,發現在界面位置存在局部原子的剪切作用,在界面處出現滑移位錯和位錯核的擴散;Weng等[20]通過模擬半共格、共格、非共格3種界面類型Cu/Ni雙金屬的拉伸過程,分析了界面類型對位錯運動以及材料力學性能的影響。羅旋等[21]研究了Ag/Ni和Cu/Ni失配位錯程度對界面力學性能的影響;程東等[22]模擬了Cu/Ni金屬在納米壓入和微摩擦過程中位錯的運動規律,認為界面失配位錯網對位錯運動的排斥阻力以及由彈性模量差而產生的界面鏡像力是位錯被限制在Cu層的微觀機理;成聰等[23]研究了Cu/Ni雙金屬在不同應變率下進行應變加載時的變形機理,發現應變率的增加有利于納米多晶結構中堆垛層錯原子團的增加,從而造成材料屈服強度的增加。上述研究主要從位錯運動的角度分析界面類型對材料力學性能的影響,而雙金屬內部位錯密度變化規律以及對材料變形的影響并未涉及。本工作在建立了不同晶格結構金屬軋制復合模型后,利用分子動力學方法模擬FeCrNi/Fe、Fe與FeCrNi軋制變形過程,對比其變形行為及規律,研究整個變形階段位錯密度變化規律及其對變形的影響,探究非共格界面對于金屬塑性變形行為的影響。
勢函數的適用性是經典分子動力學模擬首先要解決的關鍵問題。構建可靠的勢函數,需要針對具體體系進行參數擬合,因此擬合好的勢函數原則上只能用于被擬合的特定體系。而在解決實際問題的模擬過程中,所模擬體系的元素含量、晶格結構等不一定與該特定體系完全一致,需要對勢函數的適用性進行驗證。
304不銹鋼是具有典型fcc結構的奧氏體鋼,其主要成分是Fe、Cr、Ni,同時還含有微量的Mn、Nb、Mo、Ti、N等元素,其中Cr含量(質量分數,下同)為17%~19%,Ni含量8%~10%,忽略其中的微量合金元素,則Fe17Cr5Ni2與AISI-304奧氏體不銹鋼成分接近。首先建立含16384個原子的fcc-Fe模型,然后分別用Cr原子、Ni原子按一定比例隨機取代Fe原子建立304不銹鋼的初始模型,比例為Fe∶Cr∶Ni=17∶5∶2。Q235碳鋼為bcc結構,其主要成分是Fe,因此采用bcc-Fe模擬Q235碳鋼材料。
圖1 FeCrNi/Fe在勢函數1和勢函數2下馳豫過程中的結構含量
Fig.1 Contents of various lattice structures of FeCrNi/Fe in the relaxation process with potential function 1 (a) and potential function 2 (b) (The green, red and blue colors represent the fcc, hcp and bcc atoms, respectively)
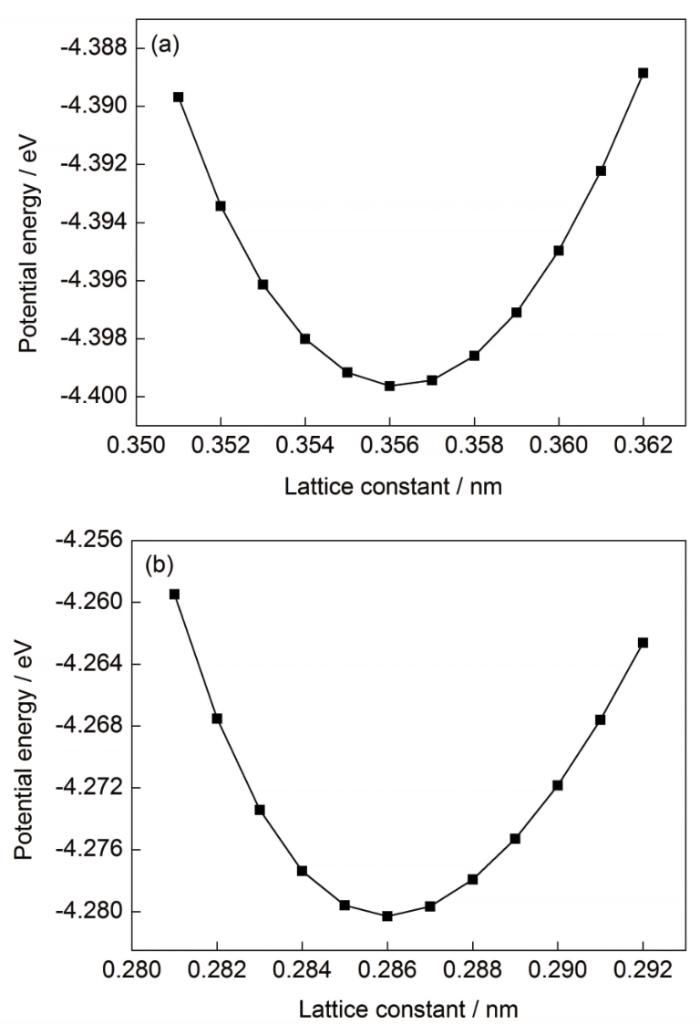
圖2 勢函數1作用下不同晶格常數FeCrNi和Fe的勢能變化
Fig.2 Potential energies of FeCrNi (a) and Fe (b) under different lattice constants with potential function 1
綜上可知,利用分子動力學方法模擬金屬軋制復合過程時,對于具有不同晶格結構的工況,本工作提出的以穩定狀態下晶格常數的一致性和晶格結構的保持度作為評價標準選擇確定最合適的勢函數,是一種簡單可行的近似解決方法。
圖3 FeCrNi/Fe模型、FeCrNi模型和Fe模型的初始構型
Fig.3 Initial configurations of FeCrNi/Fe (a), FeCrNi (b) and Fe (c)
對3種模型進行壓縮過程模擬,在600 K下沿z軸即[001]方向對樣品進行均勻壓縮,每步施加0.003的壓縮應變,直到應變為0.6為止。為了對比變形過程中3種模型的力學性能和討論壓縮過程中位錯的演化,以及分析力學性能出現差異的原因,采用位錯提取法(dislocation extraction algorithm,DXA)[28]對變形過程中位錯線總長度的變化進行定量化的統計。該方法依賴CNA技術來識別出位于位錯核的原子,然后基于拓撲連通性將這些原子組裝成位錯線分量,采用Burgers回路方法決定位錯線分量的Burgers矢量。
最后結合不銹鋼/碳鋼熱壓縮復合過程中的宏觀變形規律,討論分析分子動力學模擬所得的雙金屬微觀變形規律。
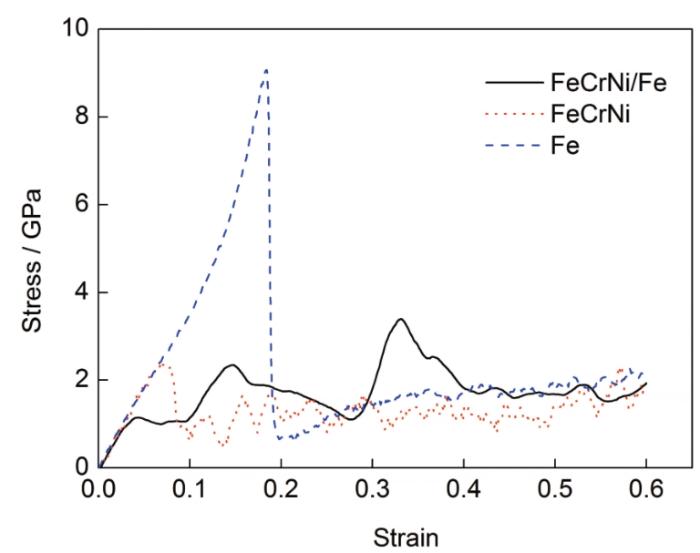
FeCrNi/Fe、FeCrNi、Fe 3種材料熱壓縮過程中微觀尺度上的應力-應變曲線如圖4所示。可以看出,在應力達到第一個峰值之前材料處于彈性變形階段,在該階段應力隨著應變線性增加,FeCrNi/Fe、FeCrNi和Fe的壓縮應變分別達到0.05、0.072、0.18時各自出現應力的第一個峰值,隨后開始進入塑性變形階段。3種材料壓縮過程中的彈性模量相同但屈服強度存在差異,其中FeCrNi/Fe的屈服強度最小,為1.15 GPa,FeCrNi、純Fe變形過程中屈服強度分別為2.37和9.07 GPa。此外,3種材料在塑性變形階段的變形形式也有所不同,FeCrNi、純Fe材料的應力在屈服點之后迅速下降,應力-應變曲線逐漸平緩,應力呈鋸齒狀的緩慢波動,而FeCrNi/Fe材料的應力-應變曲線在屈服點后開始大幅波動,應變達到0.4左右時應力才逐漸趨于平穩。
圖4 雙金屬FeCrNi/Fe、單金屬FeCrNi和Fe沿z方向壓縮的應力-應變曲線
Fig.4 Stress-strain curves for FeCrNi/Fe、FeCrNi and Fe under z-direction compression
但是,從數值上看,分子動力學模擬所得到的流變應力遠大于通過宏觀唯象實驗實測得到的應力,而且大了1~2個數量級。這可能是由于分子動力學模型對金屬材料晶體進行了無缺陷理想化假設,并且只是極小規模原子數的原子尺度建模和模擬所導致的誤差,但也是該方法目前尚難克服的不足。
2.3.1 雙金屬中的FeCrNi基體中位錯的產生與演化
FeCrNi/Fe雙金屬在變形過程中的應力-應變曲線及不同應變時的變形截圖如圖5所示,FeCrNi基體內部位錯的產生及發射過程如圖6所示。由于雙金屬界面為非共格界面,因此在弛豫結束后碳鋼基體(模型上半部分)內有大量位錯線產生,隨著應變增加至A點,FeCrNi基體靠近界面處開始有位錯出現,這意味著FeCrNi基體開始塑性變形。位錯的出現使原子間的運動變得更加容易,即要達到相同變形量時需要的應力較小,這也是應力-應變曲線開始下降的原因。不全位錯滑移后產生FeCrNi基體原子的錯排并留下堆垛層錯。隨后次級位錯開動,在滑移面上拓展并相互交錯形成Hirth阻塞。由于位錯發射路徑的一側存在堆垛層錯,一部分位錯被堆垛層錯俘獲而被永久固定住,位錯只能沿另一側發射,使得位錯的可動性降低,引起宏觀上材料的加工硬化現象。
圖5 600 K下FeCrNi/Fe沿z方向單軸壓縮作用下的應力-應變曲線以及材料變形截圖
Fig.5 Stress-strain curve and the sequence of snapshots capturing the atomic deformation process for FeCrNi/Fe under z-direction uniaxial compression at 600 K (The red, blue and yellow colors represent the Fe, Cr and Ni atoms, respectively, in FeCrNi matrix. The white color represents the Fe atoms in Fe matrix)
圖6 圖5中A~B階段,變形過程中界面處位錯向FeCrNi基體發射過程
Fig.6 Atomic configurations (a1, b1, a2, b2) and dislocation distributions (c1, c2) at point A (a1~c1) and point B (a2~c2) in Fig.5 showing the process of dislocation at the interface emitted to the FeCrNi matrix (Red color represents the hcp atoms and two adjacent hcp atoms mean an intrinsic stacking fault)
與FeCrNi、Fe相比,FeCrNi/Fe變形過程中的屈服強度最小,對于非共格界面,由于晶格常數的失配以及不同金屬晶格結構存在差異,界面對位錯起到阻礙和吸收作用,使得位錯在變形過程中不能穿過界面。另一方面,位錯在界面積累,造成界面的弱化和局部剪切效應[20]。FeCrNi/Fe模型中純Fe基體內部的位錯在界面處積累,界面處FeCrNi基體原子的局部剪切效應使得位錯的形成相比FeCrNi模型更加容易,FeCrNi基體塑性變形也變得更加容易,從而降低了FeCrNi基體的屈服強度。
2.3.2 雙金屬的純Fe基體中位錯的演化與消失
如圖7所示,在應變到達0.05 (A點)之后,FeCrNi基體開始發生變形的同時,由于FeCrNi和Fe基體變形的相互協調作用,純Fe基體內部位錯塞積開動,材料內部變形應力使純Fe基體部分原子在剪切作用下出現原子重排的現象。純Fe基體內位錯密度逐漸減小,造成B~C階段應力-應變曲線略有上升的趨勢。隨著應變增大至0.096 (C點),純Fe基體內部位錯線基本消失。晶粒取向趨于與壓縮方向一致,純Fe基體原子重排完成。
圖7 圖5中A~C階段變形過程中純Fe基體內部原子重排過程
Fig.7 Atomic configurations at point A (a), point B (b) and point C (c) in Fig.5 showing the process of atoms rearrangement of Fe matrix
2.3.3 雙金屬與單金屬變形過程中位錯演變規律對比分析
雙金屬FeCrNi/Fe變形過程中材料位錯密度分布情況如圖8a1~f1所示。可見,A~C階段,FeCrNi基體內部位錯產生并逐漸增多,與此同時純Fe基體內部發生原子重排,位錯逐漸減少。C~D階段,FeCrNi基體內部位錯形核速率大于湮滅速率,位錯密度逐漸增大形成位錯塞積,位錯之間產生交互作用,造成應力-應變曲線的上升。該階段FeCrNi/Fe的變形以FeCrNi基體的變形為主。與此同時,純Fe基體內部也有少量的位錯出現。D點以后FeCrNi基體由于位錯的塞積到了一定程度,FeCrNi基體進一步變形變得困難,純Fe基體又開始有不完全位錯出現,位錯在界面處以及頂部出現并向基體部分發射,該階段FeCrNi/Fe的變形主要以Fe基體的變形為主。E~F階段,應力上升的機理與B~C階段類似,是由于FeCrNi基體原子的重排所致。
圖8 雙金屬FeCrNi/Fe和單金屬FeCrNi變形過程中的位錯演化
Fig.8 Dislocation distributions of FeCrNi/Fe at points A~F in Fig.5, respectively, during deformation (a1~f1) and dislocation distributions of FeCrNi when the strain is 0.078, 0.1, 0.2 and 0.3, respectively (a2~d2)
可以看出,在FeCrNi和Fe基體中,整個變形過程中位錯密度呈現交替變化的規律。A~D階段,純Fe基體位錯密度的增加伴隨著不銹鋼位錯密度的減小;而D~F階段,FeCrNi基體位錯密度減小伴隨著純Fe基體位錯密度的增加。分子動力學方法模擬FeCrNi模型單金屬變形過程位錯演化過程如圖8a2~d2所示。與變形過程中雙金屬基體的位錯演化規律對比可以看出,雙金屬塑性變形階段與單一金屬相比存在很大差異,隨著應變的增加,FeCrNi模型材料內位錯線是始終存在的。
由于界面對位錯的阻礙作用,使位錯密度在基體中增大,同時界面處不斷積累的位錯產生的局部剪切作用又引起另一基體內部原子的重排,造成其位錯密度減小,形成應力-應變曲線的多峰形狀。與單金屬相比,變形過程中雙金屬原子的運動也變得困難,在塑性變形過程中抵抗塑性變形的能力得到增強。
眾所周知,位錯的滑移是金屬的主要塑性變形機制,位錯的累積運動導致宏觀的塑性變形。位錯塞積使得金屬的塑性變形變得困難,而位錯塞積的開動則有利于金屬的進一步變形。根據Zepeda-Ruiz等[6]的研究,整個流動的金屬體可以被視作一個保持穩定能量耗散速率的開放熱力學系統,該系統的機械能通過應變提供,接著通過位錯的增殖、湮滅、運動轉換為熱能,而材料的內部狀態(飽和流動應力、位錯密度)和外界應變條件(溫度、壓力、應變等)是唯一關聯的。在變形過程中,雙金屬兩基體的厚度及總位錯線長度隨應變的變化規律如圖9所示,其中圖9a中各個階段厚度的變化率代表著材料的變形能力,在雙金屬的變形過程,微觀尺度上總位錯線長度的交替變化使得兩基體的變形能力時刻發生著改變。
圖9 雙金屬FeCrNi/Fe兩基體的厚度和總位錯線長度隨應變的變化
Fig.9 Thicknesses (a) and lengths of the total dislocation line (b) of two matrices of FeCrNi/Fe under different strains
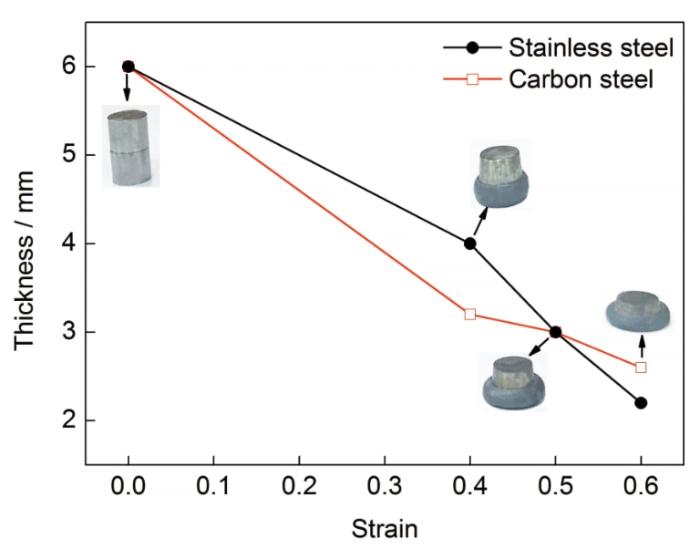
為研究雙金屬位錯演化對宏觀變形的影響,利用Gleeble3500試驗機在600 K下對AISI 304不銹鋼和Q235A碳鋼進行熱壓縮變形,材料為直徑8 mm、長6 mm圓柱形試樣,不同壓下率下不銹鋼和碳鋼的厚度變化如圖10所示。變形開始時,由于碳鋼的塑性變形能力大于不銹鋼,雙金屬的變形主要以碳鋼的變形為主,隨著變形的繼續,碳鋼基體內位錯密度逐漸增加,變形因而變得困難,不銹鋼的變形能力大于碳鋼,應變為0.5時兩基體厚度基本一致,隨后不銹鋼的變形量開始超過碳鋼。可以看出,隨著壓下量的不斷增大,不銹鋼和碳鋼基體的厚度與模擬過程中總位錯線長度均呈現出交替變化的趨勢。根據本工作對雙金屬FeCrNi/Fe變形過程中位錯密度演變的模擬結果,可以認為界面兩側位錯密度的交替變化是引起兩基體交替變形的原因。
圖10 靜壓實驗過程中各基材厚度的變化
Fig.10 Thickness variations of two base metals during deformation bonding process
(1) 針對具有不同晶格結構的2種金屬基材軋制復合變形過程,通過基于實際問題的建模和模擬計算,提出了以穩定狀態下晶格常數的準確度及晶格結構的保持度作為勢函數適用性的評價標準以及相應針對不同晶格結構材料勢函數選擇確定方法,建立了一種利用分子動力學方法模擬不同晶格結構多金屬材料彈塑性變形過程中勢函數選擇確定的近似解決辦法。
(2) 應用分子動力學方法建模及模擬不同晶格結構的FeCrNi/Fe復合過程,研究了界面對雙金屬塑性變形過程的影響,并通過與相同工況條件下單金屬變形行為進行對比,初步探索了雙金屬軋制復合過程微觀塑性變形行為及規律。
(3) 對于非共格界面,復合過程中位錯更容易在界面處形核,并使材料更容易發生變形;界面對位錯運動的阻礙作用增加了雙金屬抵抗塑性變形的能力;壓縮變形過程中,雙金屬模型2種材料位錯密度的交替變化導致了各自變形量的交替變化。
1 不同晶格結構金屬軋制復合模型的建立
1.1 勢函數的適用性驗證指標
1.2 不同晶格結構的不銹鋼/碳鋼軋制復合模型
圖1

圖2
2 非共格界面金屬軋制復合微觀變形模擬分析
2.1 建模及模擬
圖3

2.2 變形過程應力-應變關系對比分析
圖4
2.3 變形過程中位錯演變規律比較分析
圖5

圖6
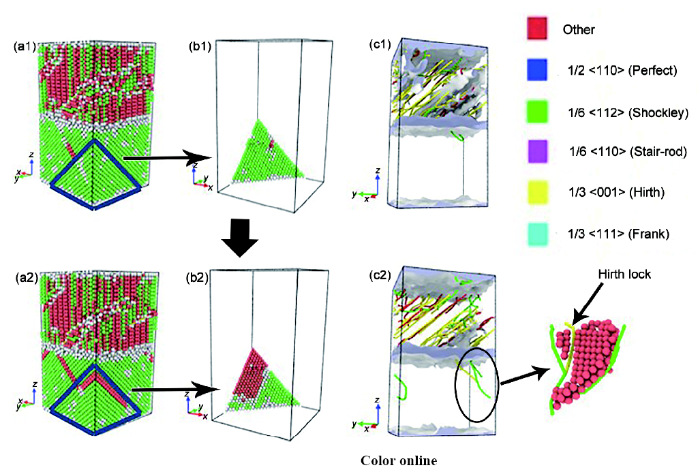
圖7

圖8

2.4 實驗對比及驗證
圖9

圖10
3 結論
來源--金屬學報
國檢檢測最新產品
同類文章排行
- 分享:
- 分享:金屬軋制復合過程微觀變形行為的分子動力學建模及研究
- 分享:B4C/6061Al復合材料熱壓縮斷裂行為的多尺度研究
- 分享:新型耐磨耐高溫氧化NiCrAlSiC復合涂層的制備及性能研究
- 分享:GH984G合金在700 ℃水蒸氣中的氧化行為
- 分享:Al-Bi合金凝固過程及微合金化元素Sn的影響
- 分享:Mo元素及熱處理對Ni2CrFeMox高熵合金在NaCl溶液中耐蝕性能的影響
- 分享:地質處置低氧過渡期X65低碳鋼腐蝕行為研究
- 分享:靜水壓力對超純Fe腐蝕行為的影響
- 分享:電磁旋流水口連鑄技術對小方坯凝固組織形貌和宏觀偏析的影響
最新資訊文章
您的瀏覽歷史









 滬公網安備31011202020290號
滬公網安備31011202020290號
