摘 要:以原位生成法制備的 TiB2 顆粒增強鐵基復合材料為研究對象,通過納米壓痕試驗及有 限元反演分析確定基體的冪硬化模型參數,建立二維細觀真實結構模型和顆粒隨機分布的體胞模 型,然后模擬單軸拉伸試驗,用等效宏觀方法計算真應力-真應變曲線,對2種模型的模擬結果進行 對比,并探討邊界條件對模擬結果的影響。結果表明:邊界條件對模擬單軸拉伸時的真應力-真應 變曲線影響較小;2種模型模擬得到單軸拉伸的真應力-真應變曲線差異較小,且與試驗結果吻合, 相對誤差小于5%;真實結構模型模擬得到的彈性模量與屈服強度的誤差小于體胞模型;不同模型 模擬得到基體與顆粒的局部微觀等效應力場及應變場有明顯差異。

關鍵詞:顆粒增強復合材料;細觀模型;有限元模擬;應力-應變曲線

中圖分類號:TG148 文獻標志碼:A 文章編號:1000-3738(2022)04-0082-07

0 引 言 

顆粒增強金屬基復合材料具有較高的強度、彈 性模量、硬度以及良好的塑性,并且生產成本低廉, 應用前景廣泛。顆粒增強金屬基復合材料在承受載 荷時的變形與失效等行為是非常復雜的,與基體和 顆粒兩相材料的性能以及二者之間的多種相互作用 密切相關。在研究微觀及細觀結構對復合材料力學 性能的影響中,采用有限元方法進行數值模擬是一 種非常有效的手段。想要進行有效的模擬,必須先要建立合理的細觀有限元模型。目前,顆粒增強復 合材料的細觀有限元模型主要有體胞模型和真實結 構模型2種。體胞模型的構建基于復合材料的結構 特征,可分為單顆粒模型及多顆粒模型[1-2]。單顆粒 模型由于其結構簡單,常用其來揭示基體、顆粒及界 面之間的作用機理,但無法探究顆粒之間的相互關 系[3]。對于多顆粒模型,可以假設顆粒是均勻分布 的,也可以使用隨機序列吸附法生成隨機分布多顆粒 模型[4]。隨機分布多顆粒模型相比于單顆粒模型雖 然考慮了顆粒間的相互作用,并且一定程度上考慮了 材料的不均勻性,但與復合材料的真實微觀結構還有 一定差異[5]。研究[6]表明,顆粒形貌越接近實際情 況,模擬結果與試驗結果的誤差越小,因此有學者發 展了基于材料真實顯微圖像的建模方式,即真實結構 模型。真實結構模型一般使用連續切片法建立,其原 理是將試樣分成很多層,取得每一層的平面結構圖像 并輸入計算機中,然后利用三維重構技術,還原出試 樣的三維真實結構[7]。由于三維真實結構模型的建 立需要復雜的前期工作并且伴隨著龐大的計算量,因 此有不少學者建立了二維真實結構模型進行模擬,得 到的模擬結果與試驗結果吻合得較好[8-11]。 體胞模型和真實結構模型各有特點,在模擬顆 粒增強復合材料的力學行為時得到的結果也有差 異,為了探究這2種模型的異同及特點,作者以原位 生成法制備的 TiB2 顆粒增強鐵基復合材料為研究 對象,通過納米壓痕試驗及有限元反演分析確定了 鐵素體基體的冪硬化模型參數,建立了二維的顆粒 隨機分布的體胞模型和真實結構模型,模擬材料在 單軸拉伸時的力學行為,研究了2種模型有限元模 擬結果的異同,并進一步探究了邊界條件對模擬結 果的影響,以期在一定程度上為顆粒增強鐵基復合 材料微觀結構的優化設計提供參考。 

1 有限元模型的建立 

1.1 材料參數的確定

在有限元建模的過程中,需要輸入復合材料各 相的材料參數。在采用原位生成的方法制備的 TiB2 顆粒增強鐵基復合材料中,鐵素體晶粒尺寸與純鐵中 的鐵素 體 晶 粒 尺 寸 不 同,而 且 晶 粒 中 會 有 位 錯 產 生[12],這導致復合材料中的鐵素體與純鐵中的鐵素 體在未受載時的初始狀態可能會有較大不同。若采 用純鐵進行單軸拉伸試驗來獲得復合材料鐵素體基 體的參數不合理,因此采用納米壓痕和有限元反演分 析的方式獲得鐵素體基體的材料屬性。將 TiB2 顆粒 視為彈性體,彈性模量為510GPa,泊松比為0.25。對 TiB2 顆粒增強鐵基復合材料進行納米壓痕試驗,測 得基體的彈性模量為214GPa,硬度為4.01GPa,然后 進一步采用 DAO 等[13]推導的量綱函數及有限元反 演分析,確定基體的單軸冪率硬化應力-應變響應曲 線。假設基體的應力σ、應變ε滿足以下關系: σ= Eε (σ ≤σy) σy 1+σEyεp n (σ >σy) ?????? (1) εr = σrEεn-1 y n1 -εy (2) 式中:E 為基體的彈性模量;σy,εy 分別為名義屈服 強度與對應的名義屈服應變;εp 為總應變減去名義 屈服應變;n 為冪硬化指數;σr、εr 分別為特征應力 與特征應變。

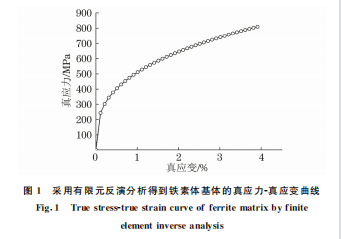
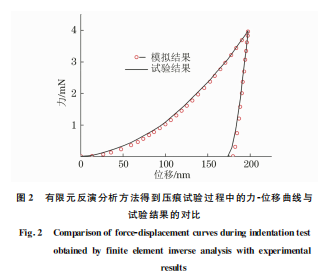
將納米壓痕試驗中采用的 Berkvich壓頭等效 成140.6°的圓錐壓頭,建立軸對稱納米壓痕有限元 模型[14]。參考 ANTUNES等[15]和 LEE 等[16]的研 究方法進行有限元反演,得到鐵素體基體的單軸真 應力-真應變曲線如圖1所示,鐵素體基體的冪硬化 指數n 為0.34,屈服強度σy 為242.91 MPa,且由圖 2可以看出,采用有限元反演分析方法得到壓痕試 驗過程中的力-位移曲線與試驗結果相吻合,驗證了 有限元反演分析方法的準確性。

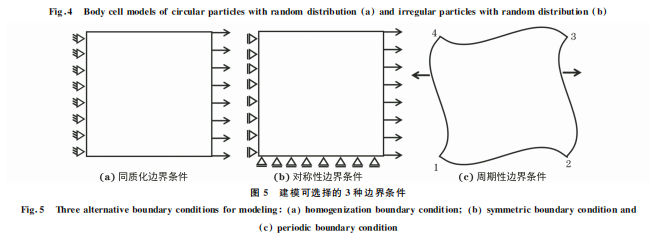
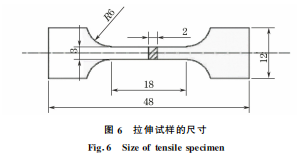
對體積分數20% TiB2 顆粒增強鐵基復合材料 建立二維代表性體積元模型。研究[11]表明,當所選 取的代表性體積元尺寸大于某一臨界值時,其所代 表的微結構能夠反映材料微觀組織的基本信息。所 選取的真實結構模型尺寸為 80μm×80μm。在 復 合 材 料 的 掃 描 電 鏡(SEM)形 貌 中 選 擇 尺 寸 為80μm×80μm 合適區域,經二值化處理轉化為矢 量文件,然后導入 ABAQUS軟件中進行建模,實現 基于微觀組織的有限元模型的建立,如圖3所示。 測得所選區域真實顆粒的平均尺寸為3μm。 體胞模型代表性體積元的建立則利用 ABAQUS 軟件進行二次開發,采用Python語言編寫程序,運行 程序建立同等顆粒尺寸、體積分數的隨機分布圓形 顆粒及不規則顆粒的體胞模型,如圖4所示。 在 ABAQUS軟件中進行有限元模擬,將 TiB2 顆粒設為彈性體,采用 CPS4R 單元劃分網格,平均 單元尺寸為0.4μm。代表性體積元模型一般可施 加3種邊界條件[17],即同質化邊界條件、對稱性邊 界條件和周期性邊界條件,如圖5所示。

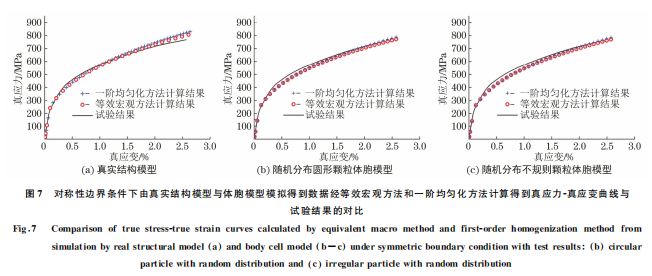
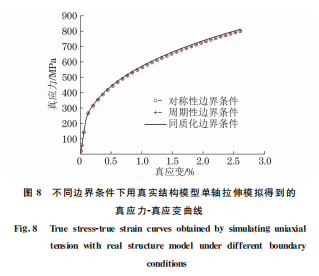
將用施加對稱性邊界條件的真實結構模型和體 胞模型模擬出的結果與單軸拉伸試驗 結 果 進 行 對 比,結果如圖7所示。由圖7可以看出,采用2種 方法得到不同模型的真應力-真應變曲線與試驗結 果較吻合,但 采 用 等 效 宏 觀 方 法 計 算 得 到 的 真 應 力-真應變曲線與試驗結果更加吻合,相對誤差小 于5%,因此 后 面 采 用 等 效 宏 觀 方 法 計 算 真 應 力- 真應變曲線,同 時 也 證 明 了 建 立 的 真 實 結 構 模 型 與體胞模型的合理性。 

2 結果與討論 

2.1 邊界條件對模擬結果的影響 

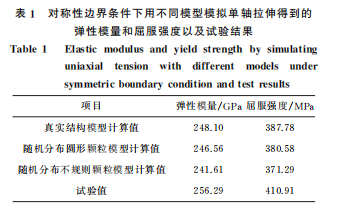
在3種邊界條件下用真實結構模型進行沿水平 方向的單軸拉伸有限元模擬,得到的拉伸真應力-真 應變曲線如圖8所示。由圖8可以看出,不同邊界 條件下模擬得到的真應力-真應變曲線基本重合,說 明邊界條件對模擬結果影響較小。

由圖9可以看出,邊界條件對約束位置的應力、 應變場具有一定影響,由于同質化邊界條件和對稱 性邊界條件對垂直加載方向的約束能力弱,使模型 變形過程中沿垂直加載方向有一定的收縮,從而導 致模型的最大應力與最大等效塑性應變位置具有較 大的差異。周期性邊界條件下模型變形均勻,在邊 界位置應力場連續性較好,與復合材料內部實際情 況相吻合。對稱性邊界條件與周期性邊界條件下的 應力與應變云圖有較高的相似性,因此單軸拉伸試 驗模擬時可用對稱性邊界條件代替周期性邊界條件 施加載荷。

2.2 2種建模方法下模擬結果的對比 

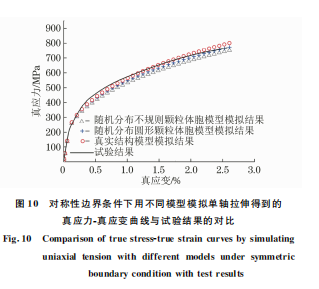
由圖10可以看出,對2種模型模擬單軸拉伸得 到的真應力-真應變曲線間差異較小,且均與試驗結 果吻合較好,相對誤差小于5%。根據真應力-真應 變曲線計算得到的屈服強度及彈性模量如表1所示。

由表1可以看出,對2種模型模擬單軸拉伸后得到 的彈性模量及屈服強度與試驗結果均相差較小,相 對誤差小于10%。從工程應用的角度來看,這兩種 模型都可以較好地模擬復合材料在單軸拉伸過程中 的應力-應變曲線。對真實結構模型模擬單軸拉伸 得到的彈性模量及屈服強度與試驗結果間的相對誤 差最小,分別為3.19%與5.63%,說明真實結構模 型在彈性模量及屈服強度模擬方面的可靠性更高。

由圖11可以看出,顆粒分布與形狀的不同導致 基體和顆粒的應力場和塑性應變場具有明顯的差 異。體胞模型對顆粒的形狀與分布進行了一定近似 處理,而真實結構模型中的顆粒具有更多的棱角, 顆粒與基體 之 間 有 較 多 的 接 觸 面 積 ,因 此 相 比 于近似化的體胞模型其內部應力集中區域較多,這也是 導致真實結構模型下在相同應變時的應力略高于體 胞模型的原因。復合材料基體高應力區域多在沿加 載方向的顆粒之間,并且顆粒間距越小,其中間的基 體等效應力越大;不同模型中基體較大的等效塑性應 變主要集中在高應力區域,并且等效塑性應變云圖與 各自的等效應力云圖具有相似性;2種模型中顆粒的 高應力區域多位于顆粒的尖角處和顆粒間距較小處。 由表2可知:真實結構模型顆粒的最大等效應力分別 為隨機分布圓形顆粒體胞模型和隨機分布不規則顆 粒體胞模型的2.22倍和2.23倍;真實結構模型基體 的最大等效塑性應變分別為隨機分布圓形顆粒體胞 模型和隨機分布不規則顆粒體胞模型的1.38倍和2. 58倍。由此可見,2種模型模擬顆粒增強金屬基復合 材料局部微觀等效應力場及應變場的結果有明顯差 異,這是由于在顆粒增強金屬基復合材料實際服役過 程中,基體常因產生較大塑性變形而失效,而顆粒則 容易在其高應力區域的尖角處發生斷裂。因此,在對 復合材料的斷裂、失效等行為進行模擬時,真實結構 模型和體胞模型的模擬結果會存在較大的差異。 

3 結 論 

(1)對原位生成法制備的TiB2 顆粒增強鐵基 復合材料建立了顆粒隨機分布的體胞模型和真實結 構模型,采用 ABAQUS軟件根據不同模型對單軸 拉伸進行有限元模擬后,采用等效宏觀方法獲取的 真 應力-真應變曲線與試驗結果基本吻合,相對誤差小于5%,驗證了這2種模型的合理性。

(2)同質化邊界條件、對稱性邊界條件和周期 性邊界條件下用真實結構模型模擬拉伸得到的真應 力-真應變曲線基本重合,說明邊界條件對模擬結果 影響較小;對稱性邊界條件下的應力與應變云圖與 周期性邊界條件相似,在單軸拉伸試驗模擬時可用 對稱性邊界條件代替周期性邊界條件施加載荷。

(3)用真實結構模型和體胞模型模擬單軸拉伸 得到的真應力-真應變曲線間差異較小,且均與試驗 結果吻合較好,相對誤差小于5%,得到的彈性模量 及屈服強度與試驗結果均相差較小,相對誤差小于 10%,且真實結構模型模擬單軸拉伸得到的彈性模量 與屈服強度的誤差小于體胞模型,說明真實結構模型 在彈性模量及屈服強度模擬方面的可靠性更高。

(4)用不同模型模擬得到復合材料基體與顆粒 在單軸拉伸時的局部微觀等效應力場及應變場有明 顯差異,真實結構模型模擬顆粒的最大等效應力分 別為隨機分布圓形顆粒體胞模型和隨機分布不規則 顆粒體胞模型的2.22倍和2.23倍,基體的最大等 效塑性 應 變 分 別 為 這 2 種 體 胞 模 型 的 1.38 倍 和 2.58倍。

參考文獻: 

[1] 陳少華.在材料研制中的連續介質細觀力學有限元建模現狀評 論[J].力學進展,2002,32(3):444-466. CHEN S H.Contimuum mesomechanical finite element modelingin materialsdevelopment:Astate-of-the-artreview [J].AdvancesinMechanics,2002,32(3):444-466. [2] 鄭陽升,楊偉苓,鄭順奇,等.顆粒增強復合材料結構的有限元 建模研究現狀[J].兵器材料科學與工程,2018,41(4):97-102. ZHENG YS,YANG W L,ZHENGSQ,etal.Researchstatus offiniteelement modelingofparticlereinforcedcomposites structure[J].Ordnance MaterialScienceand Engineering, 2018,41(4):97-102. [3] 信振洋,王悅,苗文成,等.顆粒增強金屬基復合材料參數化建 模研究[J].礦業科學學報,2020,5(1):86-95. XINZY,WANGY,MIAO W C,etal.Parametricmodelingof particlereinforced metal matrixcomposites[J].Journalof MiningScienceandTechnology,2020,5(1):86-95. [4] BAILAKANAVAR M,LIU Y,FISH J,etal.Automated modelingofrandominclusioncomposites[J].EngineeringWith Computers,2014,30(4):609-625. [5] B?HM H J,RASOOL A.Effectsofparticleshapeonthe thermoelastoplasticbehaviorofparticlereinforcedcomposites [J].InternationalJournalofSolidsandStructures,2016,87: 90-101. [6] CHAWLA N,SIDHU RS,GANESH V V.Three-dimensional visualizationandmicrostructure-basedmodelingofdeformation inparticle-reinforcedcomposites[J].Acta Materialia,2006,54 (6):1541-1548. [7] 宋衛東,王靜,劉海燕.顆粒增強復合材料真實結構有限元建模 [J].北京理工大學學報,2009,29(6):501-505. SONG W D,WANGJ,LIU H Y.Finiteelementmodelofreal structureforparticlereinforcedcomposites[J].Transactionsof BeijingInstituteofTechnology,2009,29(6):501-505. [8] 邵軍超,劉越.顆粒增強金屬基復合材料力學行為有限元模擬 研究現狀[J].材料導報,2007,21(9):111-115. SHAOJC,LIU Y.Areviewoffiniteelementsimulationson themechanicalbehaviorforparticlesreinforced metalmatrix composites[J].MaterialsReview,2007,21(9):111-115. [9] LATYPOV M I,SHIN S,DE COOMAN B C,et al. Micromechanicalfiniteelementanalysisofstrainpartitioning inmultiphasemedium manganeseTWIP+TRIPsteel[J].Acta Materialia,2016,108:219-228. [10] 王駿思.鐵素體/貝氏體雙相鋼在循環載荷作用下變形行為的 模擬研究[D].秦皇島:燕山大學,2019:34-45. WANGJS.Simulationstudy on deformation behaviorof ferrite/bainitedual-phase steelundercyclicloading[D]. Qinhuangdao:YanshanUniversity,2019:34-45. [11] 申剛.雙相鋼連續退火過程組織演變的計算模擬[D].上海: 上海交通大學,2018:35-55. SHEN G.Simulation of microstructure evolution during intercriticalannealing ofcold-rolled dual-phasesteel[D]. Shanghai:ShanghaiJiaotongUniversity,2018:35-55. [12] WANGB X,QIU F,CUI W W,etal.Microstructureand tensilepropertiesofgraphiteductileironimprovedbyminor amountofdual-phasedTiC-TiB2 nanoparticles[J].Advanced EngineeringMaterials,2021,23(8):2100246. [13] DAO M,CHOLLACOOP N,VAN VLIET K J,et al. Computationalmodelingoftheforwardandreverseproblems ininstrumentedsharpindentation[J].ActaMaterialia,2001, 49(19):3899-3918

< 文章來源>材料與測試網 > 機械工程材料 > 46卷 >