梅益1, , 孫全龍1, 喻麗華1, 王傳榮2, 肖華強1

1 貴州大學(xué)機械工程學(xué)院 貴陽 550025
2 中國石油新疆獨山子石化分公司 克拉瑪依 833699

摘要

關(guān)鍵詞： 鋁合金 ; 微觀組織 ; 晶粒尺寸 ; 極限學(xué)習(xí)機 ; GA-ELM模型

晶粒尺寸是決定材料機械性能最本質(zhì)的因素之一,對鋁合金壓鑄件晶粒尺寸的控制是獲得高質(zhì)量壓鑄件的關(guān)鍵。在考慮到壓鑄件缺陷最小的同時,在實際的壓鑄工藝制定過程中應(yīng)選取獲得最小平均晶粒尺寸的壓鑄工藝參數(shù)。因此,鋁合金壓鑄件晶粒尺寸的有效預(yù)測對合理制定壓鑄工藝參數(shù)、提升產(chǎn)品質(zhì)量具有重要意義。

傳統(tǒng)的晶粒尺寸預(yù)測方法包括利用模擬軟件進行模擬、經(jīng)驗法等[1,2]。模擬軟件進行模擬的預(yù)測方法是應(yīng)用Anycasting或Procast等鑄造過程仿真軟件對鑄件晶粒尺寸進行預(yù)測,Anycasting或Procast等鑄造過程仿真軟件是采用基于有限元(FEM)的數(shù)值計算和綜合求解的方法,對鑄件充型、凝固和冷卻過程提供模擬,基于強大的有限元分析及微觀組織模塊,它能夠較為準(zhǔn)確地預(yù)測鋁合金壓鑄件成型的晶粒尺寸,但是它的問題是,面對復(fù)雜鑄件時,計算的耗時非常長,晶粒尺寸預(yù)測效率低[3,4];經(jīng)驗法是指壓鑄工藝人員通過自身的生產(chǎn)經(jīng)驗對某組壓鑄工藝參數(shù)條件下將得到的鑄件的晶粒尺寸提前預(yù)測,根據(jù)經(jīng)驗匹配最優(yōu)工藝參數(shù)組合以獲取晶粒尺寸最小的鑄件。經(jīng)驗法耗時短、效率高,但是它的問題是非常依賴于工藝人員自身經(jīng)驗及技術(shù)水平,對壓鑄件晶粒尺寸的預(yù)測精度很低[5]。針對傳統(tǒng)的晶粒尺寸預(yù)測方法存在的問題,訾炳濤等[6]和劉彬等[7]提出了應(yīng)用BP神經(jīng)網(wǎng)絡(luò)算法模型預(yù)測鑄件晶粒尺寸的方法,雖然該方法在一定程度上解決了傳統(tǒng)的晶粒尺寸預(yù)測方法效率與精度不能兼得的問題,但是該模型自身存在易陷入局部最優(yōu)解、網(wǎng)絡(luò)結(jié)構(gòu)不易確定的問題,進而影響了預(yù)測精度;唐江凌等[8]提出了應(yīng)用支持向量機算法模型預(yù)測合金晶粒尺寸的方法,該模型具有擬合精度高、泛化能力強的優(yōu)點,但是也存在參數(shù)確定困難的問題,進而影響了預(yù)測效率;傳統(tǒng)的學(xué)習(xí)算法(如BP算法、支持向量機等)固有的一些缺點,成為制約其發(fā)展的主要瓶頸,也阻礙了其在晶粒尺寸預(yù)測方面的應(yīng)用。Huang等[9]針對傳統(tǒng)算法的固有缺點提出了一種特殊的單隱含層前饋神經(jīng)網(wǎng)絡(luò)模型-極限學(xué)習(xí)機,與傳統(tǒng)算法相比,該算法具有參數(shù)設(shè)置少、學(xué)習(xí)速度快和泛化性能好的優(yōu)點,但是該算法隨機產(chǎn)生輸入層到隱含層的權(quán)值矩陣及隱含層閾值矩陣,對結(jié)果影響較大,不易獲得最優(yōu)極限學(xué)習(xí)機(ELM)模型進行預(yù)測[10]。因此,需要找到一種適用于這類復(fù)雜問題的方法,準(zhǔn)確、高效地預(yù)測鋁合金壓鑄件晶粒尺寸。

本工作研究了一種結(jié)合遺傳算法(GA)和極限學(xué)習(xí)機(ELM)的GA-ELM模型,分別利用GA-ELM模型、原始ELM模型和BP神經(jīng)網(wǎng)絡(luò)模型,對相關(guān)實驗數(shù)據(jù)進行擬合及預(yù)測,并對比三者的擬合精度和效率,以證明GA-ELM模型的有效性和實用性。

1 GA-ELM流程

1.1 ELM基本原理

ELM是一種特殊的單隱含層前饋神經(jīng)網(wǎng)絡(luò)模型,它的輸入層權(quán)值矩陣和隱含層閾值矩陣是隨機產(chǎn)生的,并且在之后的運算中無需調(diào)整。研究[11,12]表明,只需要設(shè)置隱含層節(jié)點的數(shù)量,便可以獲得唯一的最優(yōu)解。

對于給定的輸入樣本X,隱含層神經(jīng)元的輸出矩陣H的計算公式為[11]：

$\begin{array}{c}?=?(?{?}^{?}+?)\end{array}$(1)

式中,W為輸入層權(quán)值矩陣,b為隱含層閾值矩陣,W和b隨機產(chǎn)生;g為隱含層神經(jīng)元激活函數(shù)。

ELM神經(jīng)網(wǎng)絡(luò)的輸出值P為[11]：

$\begin{array}{c}?=\left({?}^{?}?\right)\end{array}$(2)

式中,β為隱含層到輸出層的權(quán)值矩陣,只要確定β即可唯一確定ELM神經(jīng)網(wǎng)絡(luò)。

對于給定的訓(xùn)練輸出樣本Y,用輸出樣本替代網(wǎng)絡(luò)輸出值,則β可以通過求解以下方程組的最小二乘解獲得[11]：

$\begin{array}{c}\underset{?}{\mathit{min}}‖{?}^{?}?-?‖\end{array}$(3)

方程組(3)的最小二乘解 $\begin{array}{c}\stackrel{\wedge }{?}\end{array}$為[11]：

$\begin{array}{c}\stackrel{\wedge }{?}=({?}^{?}{)}^{+}?\end{array}$(4)

式中,(HT)+為轉(zhuǎn)置矩陣HT的Moore-Penrose廣義逆。

1.2 GA優(yōu)化ELM模型

由以上ELM基本原理可知,W和b可隨機產(chǎn)生。因此在隱含層節(jié)點相同的條件下,使用同一個訓(xùn)練樣本集訓(xùn)練ELM模型,由于W和b隨機產(chǎn)生,會造成網(wǎng)絡(luò)擬合出的晶粒尺寸變化很大。GA具有很強的全局尋優(yōu)能力,利用GA為ELM模型尋找最優(yōu)的初始W和b,可以提高ELM模型的擬合精度,獲取最優(yōu)ELM模型。

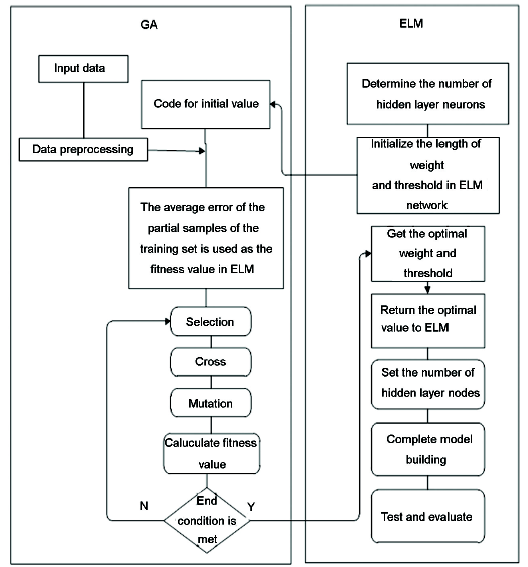
GA-ELM訓(xùn)練步驟如下：

(1) 首先讀入實驗數(shù)據(jù)。將實驗數(shù)據(jù)分成訓(xùn)練集和測試集,并將數(shù)據(jù)進行歸一化處理,避免因?qū)嶒灁?shù)據(jù)數(shù)量級相差較大而造成預(yù)測誤差較大。

(2) 調(diào)用GA尋找ELM算法最優(yōu)的初始W和b。種群中的每個個體都包含了一個ELM網(wǎng)絡(luò)的所有權(quán)值和閾值,個體通過適應(yīng)度函數(shù)計算個體適應(yīng)度值,遺傳算法通過選擇、交叉和變異操作找到最小適應(yīng)度值的對應(yīng)個體。個體適應(yīng)度函數(shù)取為ELM網(wǎng)絡(luò)對訓(xùn)練集中部分樣本預(yù)測的平均誤差[11]：

$\begin{array}{c}\mathit{error}=\frac{\sum ^{}\left|{?}_{\mathit{ij}}-{?}_{\mathit{ij}}\right|}{?}\end{array}$(5)

式中,yij為訓(xùn)練集中部分樣本的輸出預(yù)測值,xij為訓(xùn)練集部分樣本真值,N為訓(xùn)練集部分樣本個數(shù)。

(3) 用遺傳算法得到最優(yōu)個體對ELM的初始權(quán)值和閾值賦值,并設(shè)置隱含層節(jié)點個數(shù),完成GA-ELM模型的建立。

(4) 利用測試集樣本對GA-ELM模型進行測試及效果評價。其算法流程如圖1所示。

圖1   遺傳算法-極限學(xué)習(xí)機(GA-ELM)算法流程

Fig.1   An algorithm flow of genetic algorithms-extreme learning machine (GA-ELM)

2 基于GA-ELM的鋁合金壓鑄件晶粒尺寸預(yù)測模型

2.1 訓(xùn)練集樣本數(shù)據(jù)的獲取

首先,選取與凝固過程密切相關(guān)的壓鑄工藝參數(shù)作為輸入?yún)?shù),輸入?yún)?shù)選定為模具預(yù)熱溫度TP、壓射溫度TI、低速充型速度VS和高速充型速度VF 4個參數(shù);然后,由于壓鑄件不同位置晶粒尺寸不相同,所以選取鑄件上對機械性能要求較高的部位截面的平均晶粒尺寸作為輸出參數(shù);最后,通過實際壓鑄生產(chǎn),對不同的輸入?yún)?shù)進行實驗,獲得相應(yīng)壓鑄件,對其進行金相分析后獲得不同條件下的平均晶粒尺寸。

圖2   汽車空壓機端蓋壓鑄件幾何模型

Fig.2   Geometric model of die casting of automobile air compressor end cover

以汽車空壓機端蓋的壓鑄成型為例,其幾何模型如圖2所示。輪廓尺寸112 mm×112 mm×84 mm,平均壁厚5 mm,材料為鋁合金ADC12。汽車空壓機端蓋接口部位幾何模型如圖3所示。此部位要求常溫下力學(xué)性能優(yōu)良,晶粒尺寸細(xì)小,因此選取該部位中間截面的平均晶粒尺寸(以下簡稱晶粒尺寸)作為實驗的輸出參數(shù),同時根據(jù)壓鑄生產(chǎn)經(jīng)驗確定模擬實驗的輸入?yún)?shù)及水平設(shè)置,如表1所示。

圖3   汽車空壓機端蓋接口部位幾何模型

Fig.3   Geometric model of the joint of automobile air compressor end cover

采用四因素四水平正交實驗法對該鑄件的壓鑄工藝方案進行優(yōu)化設(shè)計,即L32(45)正交表,共32組實驗。利用這32組壓鑄工藝方案進行實際壓鑄生產(chǎn),對生產(chǎn)得到的壓鑄件進行金相實驗并測量其晶粒尺寸,獲得不同工藝參數(shù)條件下的晶粒尺寸,這32組樣本作為訓(xùn)練集,工藝參數(shù)的正交實驗表及晶粒測量結(jié)果如表2所示。遺傳算法優(yōu)化中的個體適應(yīng)度值取為訓(xùn)練集中No.27~No.32共6個樣本的預(yù)測平均誤差值。

2.2 GA-ELM參數(shù)設(shè)置

利用表2中的訓(xùn)練集樣本數(shù)據(jù)對GA-ELM算法模型進行訓(xùn)練。GA-ELM模型完整地保留了GA和ELM算法中的可調(diào)參數(shù),這些參數(shù)的選取可以參考ELM和GA算法的相關(guān)文獻[13~26]。本工作通過多次調(diào)整相關(guān)參數(shù),將得到的最終的實驗結(jié)果進行對比,給出效果最好的一組推薦值,如表3所示。

2.3 測試集樣本數(shù)據(jù)的獲取

測試集樣本數(shù)據(jù)工藝參數(shù)的選取如表4所示,同樣通過壓鑄生產(chǎn)實驗獲得相應(yīng)晶粒尺寸。

2.4 預(yù)測效果及分析

遺傳算法優(yōu)化的進化結(jié)果如圖4所示,即為個體適應(yīng)度值變化曲線。可以看出,遺傳算法部分收斂得很好,在30代時已基本收斂至最優(yōu)權(quán)值和閾值。由于其權(quán)值矩陣和閾值矩陣規(guī)模較大,其具體取值不再贅述。

圖4   遺傳算法進化結(jié)果

Fig.4   Evolution consequences of the GA optimization

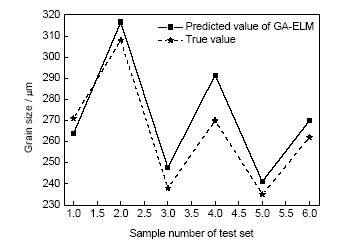
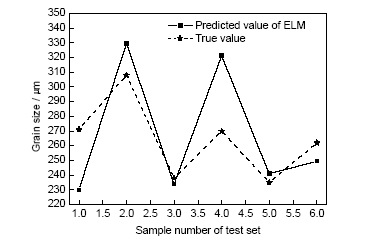
利用建立完成的GA-ELM模型對測試集數(shù)據(jù)進行預(yù)測,并與測試集輸出真值進行對比,如圖5所示。可以看出,除第4組樣本外,其它測試集樣本誤差均控制在10 μm以內(nèi),第4組樣本誤差也不超過22 μm。考慮到本工作研究微觀尺寸下的晶粒,微觀尺寸內(nèi)存在一定的擾動因素,并且訓(xùn)練使用的樣本數(shù)量較少,擬合度有限,因此不超過22 μm的最大誤差屬于可以接受的最大誤差值。同時,通過計算,測試集樣本數(shù)據(jù)預(yù)測平均絕對誤差為10.2 μm,平均相對誤差為3.8%。可見,GA-ELM模型可以準(zhǔn)確、有效地對晶粒尺寸進行預(yù)測。

圖5   GA-ELM模型對測試集樣本的預(yù)測結(jié)果與測試集輸出真值對比

Fig.5   Comparisons between predicted results of GA-ELM model and output true values of test set

2.5 與其它模型預(yù)測結(jié)果對比

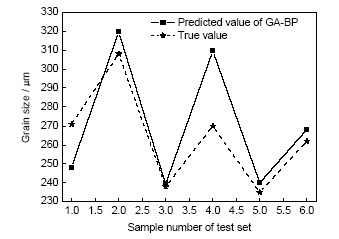
為了體現(xiàn)該模型的優(yōu)越性,采用GA-BP神經(jīng)網(wǎng)絡(luò)及原始ELM模型對該樣本進行預(yù)測,其中原始ELM模型隱含層節(jié)點數(shù)為60 (多次實驗確定),隱含層激勵函數(shù)選擇“sigmoid”函數(shù);GA-BP神經(jīng)網(wǎng)絡(luò)模型隱含層節(jié)點數(shù)設(shè)為25 (多次實驗確定),隱含層激勵函數(shù)選擇“logsig”函數(shù)。GA-BP神經(jīng)網(wǎng)絡(luò)模型及原始ELM模型的測試集樣本預(yù)測結(jié)果及輸出真值分別如圖6和7所示。

圖6   GA-BP模型對測試集樣本的預(yù)測結(jié)果與測試集輸出真值對比

Fig.6   Comparisons between predicted results of GA-BP model and output true values of test set

圖7   ELM模型對測試集樣本的預(yù)測結(jié)果與測試集輸出真值對比

Fig.7   Comparisons between predicted results of ELM model and output true values of test set

以上3種模型的預(yù)測結(jié)果對比情況見表5。可以看出,GA-ELM模型在預(yù)測精度上要明顯優(yōu)于其它2個模型。但由于采用了遺傳算法,GA-ELM模型的訓(xùn)練效率要遠(yuǎn)低于原始ELM模型。但是,即使如此,GA-ELM模型的訓(xùn)練效率也要遠(yuǎn)高于GA-BP模型,其效率是可以接受的。綜上所述：GA-ELM模型具有較高的預(yù)測精度,可以相對準(zhǔn)確地預(yù)測鋁合金壓鑄件的晶粒尺寸。但該模型的預(yù)測效率相對較低,雖然可以接受,但還有提高空間。

3 實驗驗證

為驗證GA-ELM算法可靠性,制定一組壓鑄工藝參數(shù)進行實驗驗證。TP設(shè)為660 ℃,TI設(shè)為210 ℃,VS設(shè)為0.3 m/s,VF設(shè)為5 m/s,通過GA-ELM模型預(yù)測該組壓鑄工藝參數(shù)對應(yīng)的晶粒尺寸D,預(yù)測值為267 μm。同時,對該壓鑄工藝參數(shù)條件下生產(chǎn)的汽車空壓機端蓋的接口部位的金相組織進行觀察及幾何測量,選取同一截面的3個不同部位,其金相組織如圖8所示。通過截線法分別獲得3個位置的平均晶粒尺寸后,將這3個值再次平均代表整個截面的平均晶粒尺寸,為258.5 μm,與GA-ELM模型預(yù)測值相差8.5 μm,相對誤差為3.18%。可見,GA-ELM模型預(yù)測效果極好。

圖8   汽車空壓機端蓋接口部位同一截面不同位置的金相組織

Fig.8   Metallographic microstructures of different positions (a~c) on the same cross-section of the joint of automobile air compressor end cover

4 結(jié)論

(1) 提出了應(yīng)用遺傳算法-極限學(xué)習(xí)機(GA-ELM)模型預(yù)測鋁合金壓鑄件晶粒尺寸的方法。采用GA對ELM的輸入層權(quán)值矩陣和隱含層閾值矩陣進行優(yōu)化,避免了輸入層權(quán)值矩陣和隱含層閾值矩陣隨機性對ELM預(yù)測精度的影響,提高了預(yù)測準(zhǔn)確率。豐富了鋁合金壓鑄件晶粒尺寸預(yù)測方法。

(2) GA-ELM模型是一種高精度、較高效、滿足工程要求的模型。其預(yù)測精度高于GA-BP模型和原始ELM模型,訓(xùn)練效率高于GA-BP模型,但低于原始ELM模型。

(3) 通過實際壓鑄生產(chǎn)及金相組織測量實驗,驗證了GA-ELM模型預(yù)測鋁合金壓鑄件晶粒尺寸的可靠性。

來源--金屬學(xué)報