分享:預循環應力對高速列車關鍵結構用鋁合金材料疲勞裂紋擴展行為的影響
沈陽建筑大學機械工程學院 沈陽 110168
對服役多年的高速列車關鍵結構用鋁合金材料進行斷裂力學性能測試,探究其穩態擴展區域和近門檻值區域的疲勞裂紋擴展行為,闡釋服役材料力學行為的變化規律。鑒于服役材料疲勞裂紋擴展行為的折線特征,開展不同水平預循環應力作用下的斷裂力學實驗研究,剖析預循環應力對材料斷裂力學性能“鍛煉”效應的影響,建立合理的壽命預測模型,并與實測數據進行對比。研究表明:服役材料在穩態裂紋擴展階段的疲勞裂紋擴展行為呈折線特征,近門檻值區域的延遲擴展行為是促使折線現象產生的原因;經歷預循環應力作用后,材料疲勞裂紋擴展速率與應力強度因子范圍(da/dN-ΔK)的關系曲線在穩態裂紋擴展的初期階段呈現類似服役材料的折轉行為;不同水平的預循環應力對材料斷裂力學性能的“鍛煉”效果不同,存在能夠使材料達到最佳“鍛煉”效果的預循環應力水平;對于折轉型da/dN-ΔK關系曲線,本工作所建立的計算模型能夠更加準確地預測材料的疲勞裂紋擴展壽命。
關鍵詞:
高速列車在運行過程中始終經歷復雜環境因素的影響,同時承受隨機循環載荷的作用,使其服役性能下降,給高速列車的安全保障和系統維護帶來了極大的挑戰[1]。隨著服役年限的延長,高速列車關鍵結構部件的性能會發生改變,實際使用中有時也因零部件損傷而引發重大事故。因此,高速列車關鍵結構部件在經歷一段時間的服役過程后還能否保證結構安全成為人們關注的焦點之一[2,3],探索提高結構材料強度和使用壽命的途徑也成為重要的研究課題[4]。
20世紀80年代至今,針對高速列車的服役安全問題,研究人員采用損傷容限技術對高速列車結構疲勞、服役安全控制等問題進行了大量基礎性研究[5,6,7,8,9,10,11]。Beretta等[6]通過實驗手段和數值分析方法建立了車軸疲勞裂紋擴展的隨機模型。Regazzi等[7]考慮了殘余應力對車軸疲勞裂紋擴展行為的影響,建立了基于無交互載荷作用條件下的疲勞裂紋擴展壽命預測模型。Liu等[8]應用累積損傷理論,評估了高速列車車輪的尺寸效應、載荷類型以及材料的硬度對疲勞壽命的影響。伴隨我國“大提速”戰略的實施,國內研究人員對高速列車結構部件的疲勞斷裂問題也進行了大量研究。文獻[9,10]針對車軸材料進行一系列實驗研究,建立了基于車軸鋼的隨機應力-壽命(S-N)關系概率模型、循環本構概率模型、局部Basquin S-N的關系模型以及疲勞長裂紋擴展概率模型。Zhou等[11]應用超長壽命疲勞可靠性方法和疲勞長裂紋擴展模型,估算了車軸的超長服役壽命和臨界安全裂紋尺寸。
針對高速列車服役過程中的承載問題,儲軍等[12]研究表明,載荷會對結構材料造成損傷,但低于疲勞極限一定范圍內的低幅載荷(本工作稱之為預循環應力)卻能夠對結構材料的強度起到強化作用,即低載“鍛煉”作用。20世紀20年代,Gough[13]通過實驗手段最早提出了有關低載“鍛煉”效應的概念。20世紀70年代,Hironobu等[14,15]研究發現,低載“鍛煉”作用的顯著程度與施加的載荷水平有關。20世紀末,Ishihara和McEvily[16]通過實驗發現施加高于疲勞極限的循環載荷也會對材料起到“鍛煉”作用,并指出高于疲勞極限的第一級循環載荷對材料的“鍛煉”效果最為明顯。在我國,20世紀60年代,西安交通大學針對不同金屬材料進行了一次大規模的低載“鍛煉”實驗研究,開啟了我國在此領域的研究先河[17]。隨后,吳志學等[18]提出,存在能夠使材料達到最佳“鍛煉”效果的臨界載荷值,當后期施加的載荷大于此臨界值時,對材料的“鍛煉”效應逐漸消失。20世紀90年代起,Zheng等[19,20,21]揭示了汽車零部件低載“鍛煉”次數與材料疲勞強度的關系,并建立了疲勞壽命、“鍛煉”載荷以及“鍛煉”次數的三維曲面方程。
綜上所述,以往對于高速列車服役安全的研究主要集中在車軸、車輪以及轉向架構架等主要承載部件。相比較而言,針對高速列車端部底架結構疲勞損傷的理論研究和實驗研究較少。同時,對于材料受到低載強化作用而產生“鍛煉”效應的相關研究都是基于低幅載荷對材料疲勞性能的影響,很少開展低幅載荷對材料斷裂力學性能的影響研究。因此,本工作針對高速列車端部底架關鍵功能部件鋁合金材料進行斷裂力學性能測試與可靠性分析,重點圍繞服役經歷對材料斷裂力學性能的影響、預循環應力對材料斷裂力學性能產生的“鍛煉”效應以及材料疲勞裂紋擴展壽命的評估方法等開展系統研究,為高速列車的可靠性設計和安全性運行提供基礎科學依據。
1 實驗方法
針對服役6 a的高速列車車體端部底架結構開展研究,端部底架結構承受車體施加的載荷,如圖1a所示,其表面經噴漆防腐處理后,裸露在車體外部,直接與外部環境接觸。在長期的服役過程中,經歷不同區域、季節更替等復雜的服役環境,經受腐蝕、潮濕、溫度變化及受載等交替作用影響。
圖1
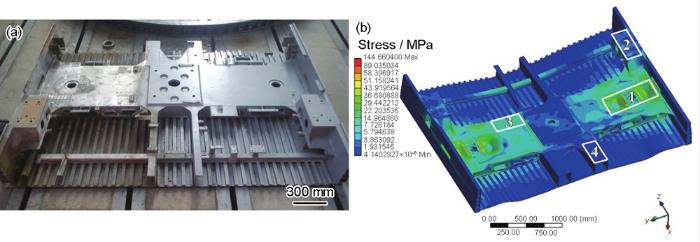
圖1 高速列車端部底架實物圖和有限元數值分析及取樣圖
Fig.1 Photo of the chassis of high speed train (a) and finite element method (FEM) stress analysis and schematic diagram of sampling method (b) (1—sheet material, 2—anti-snake movement damper seat, 3—section bar, 4—draw beam)
Color online
選取端部底架結構中4個關鍵功能部件作為研究對象。其中,枕梁板材和抗蛇行減振器座為7N01鋁合金T4態(固溶熱處理后自然時效至基本穩定的狀態);枕梁型材和牽引梁為7N01鋁合金T5態(高溫成型過程冷卻后進行人工時效的狀態)。根據底架結構的幾何尺寸及服役狀態下運行參數的有限元數值分析結果,得到如圖1b所示各功能部件服役過程中的應力分布情況,并以此確定試樣的取樣位置。7N01鋁合金的化學成分(質量分數,%)測試結果為:Zn 4.64,Mg 1.01,Cu 0.12,Mn 0.31,Zr 0.11,Cr 0.15,Fe 0.23,Si 0.12,Al 余量。
疲勞裂紋擴展實驗采用GB/T 6398-2000《金屬材料疲勞裂紋擴展速率試驗方法》中推薦的標準三點彎曲試樣[22]。利用線切割方法預制試樣裂紋前緣缺口,缺口深度為7 mm,試樣長度為140 mm,寬度為30 mm,厚度為10 mm,跨距為120 mm。試樣設計尺寸如圖2所示。
圖2
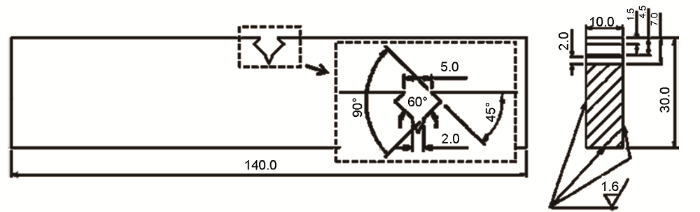
圖2 標準三點彎曲試樣
Fig.2 Dimensional drawing of standard three-point bend specimen (unit: mm)
疲勞裂紋擴展實驗在實驗室空氣環境條件下進行,使用Instron 8800型電液伺服疲勞試驗機進行測試。實驗采用正弦波加載方式,恒應力比為0.1,為了保證結果的穩定性,控制頻率為10 Hz。預制疲勞裂紋時,將最大載荷(Pmax)的誤差控制在5%以內,每一級降載不大于20%,預制裂紋長度約為2 mm。穩定擴展過程中始終保持恒定載荷范圍(ΔP,本實驗選定的ΔP為預制疲勞裂紋擴展階段的最后一級載荷范圍值)。采用夾式引伸計對裂紋尖端進行實時跟蹤測量并記錄整個裂紋擴展過程,以此獲得若干組裂紋擴展長度與循環周次(a-N)的關系數據。在試樣完全斷裂前,終止裂紋進一步擴展,完成實驗。
對預循環應力作用下的疲勞裂紋擴展行為研究同樣選取7N01鋁合金材料(未經歷服役的初始狀態材料)。首先截取母材尺寸為200 mm×50 mm×10 mm的寬板進行疲勞極限下的預循環應力疲勞實驗。選取經歷預循環應力作用且未發生疲勞失效的材料加工成標準三點彎曲試樣進行疲勞裂紋擴展速率實驗。
使用QBG-100高頻疲勞試驗機,在應力比為0的情況下,對選用的7N01鋁合金材料進行疲勞極限測試,其結果為159 MPa。截取7N01鋁合金母材進行疲勞極限下不同預循環應力的疲勞實驗,預循環應力水平分別取0 (未經歷預循環應力作用的初始狀態材料)、30、60、90和120 MPa,每組試樣數量為3個,循環方式為脈動循環,應力比為0,預循環周次為107 cyc,預循環應力為30、60、90和120 MPa時所對應的實驗頻率分別為183.4、181.7、183.9和184.5 Hz。將經歷預循環應力作用且未失效的材料加工成標準三點彎曲試樣,用于疲勞裂紋擴展實驗測試,其實驗過程、實驗條件以及裂紋擴展長度的測量計算方法與上文服役材料的疲勞裂紋擴展實驗方法一致。
2 實驗結果
2.1 穩態擴展階段疲勞裂紋擴展行為特性
應用Paris公式描述穩態疲勞裂紋擴展階段裂紋擴展速率(da/dN)與應力強度因子范圍(ΔK)的關系[23,24],其表達式為:
式中,a為裂紋長度;N為應力循環次數;C、m為材料常數。
ΔK表達式為[22]:
其中,
式中,B為試樣厚度;W為試樣寬度;
建立da/dN與ΔK關系的對數坐標系,將式(1)兩邊分別取對數,則有:
由式(4)可見,da/dN-ΔK實驗數據在雙對數坐標系下呈現線性關系,采用最小二乘法對lg(da/dN)-lg(ΔK)數據進行線性擬合,獲得的擬合曲線為Paris曲線,其中lgC和m分別為Paris曲線的截距和斜率。
圖3給出了服役材料和原始材料(未經歷服役的初始狀態材料)穩態裂紋擴展階段da/dN-ΔK的關系以及擬合獲得的理論Paris曲線。疲勞裂紋擴展實驗數據表明,da/dN隨ΔK的增大而增大。服役材料的da/dN-ΔK關系曲線整體高于原始材料,長期服役促使材料抵抗裂紋擴展的能力有所下降,疲勞裂紋擴展速率提高。可以看出,原始材料的da/dN-ΔK關系曲線近似成線性關系,與理論Paris曲線(圖3中實線部分)能夠較好地吻合。服役材料的da/dN-ΔK關系曲線在穩態裂紋擴展階段呈折線形式,穩態裂紋擴展初始階段曲線的da/dN對ΔK較為敏感,在較小的ΔK內da/dN呈現快速上升的趨勢。說明此階段服役材料抵抗裂紋擴展的能力優于原始材料,在相同的da/dN下,服役材料需要更大的裂紋擴展驅動力。經歷了一段時間的啟裂后,服役材料的da/dN-ΔK關系曲線呈快速上升趨勢,在經過折線現象的轉折點后,其疲勞裂紋擴展行為規律趨于穩定。對比不同熱處理工藝的服役材料,T4態7N01鋁合金da/dN-ΔK關系曲線的轉折程度更加顯著,呈現出明顯的雙線性關系,T5態7N01鋁合金的轉折程度相對平緩。
圖3
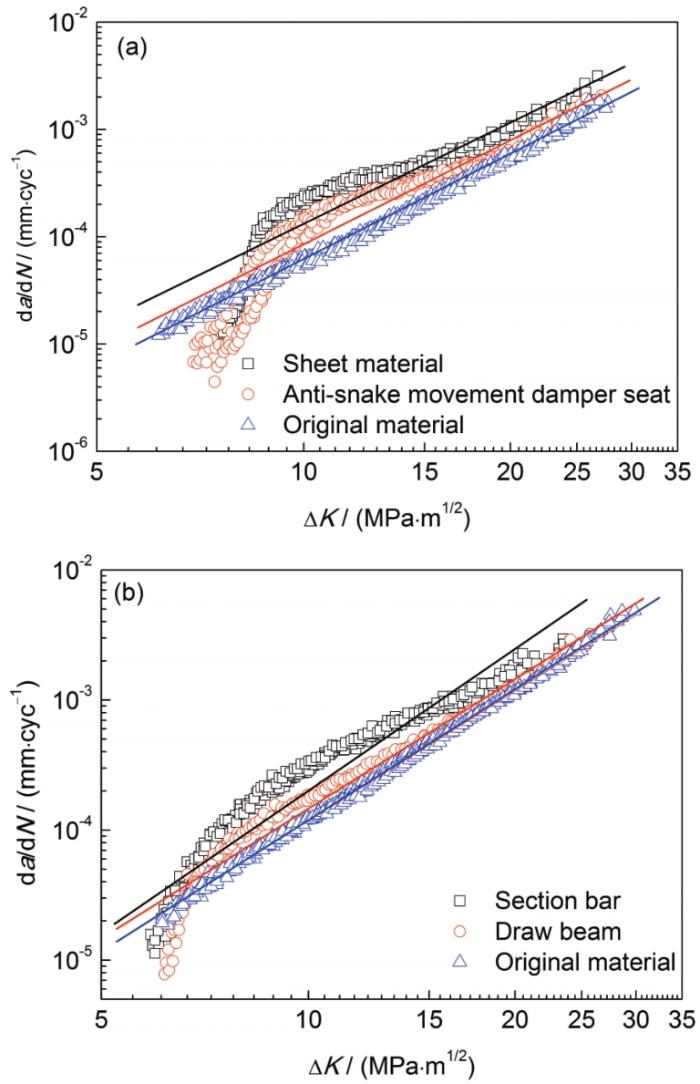
圖3 穩態裂紋擴展階段裂紋擴展速率與應力強度因子范圍(da/dN-ΔK)關系曲線
Fig.3 Fitted curves of crack propagation rates vs stress intensity factor range (da/dN-ΔK) in the steady growth zone
(a) 7N01-T4 (b) 7N01-T5
2.2 近門檻值區域疲勞裂紋擴展行為
以枕梁板材和原始材料為例,圖4給出考慮近門檻值區域的da/dN-ΔK關系曲線。根據服役材料和原始材料的疲勞裂紋擴展行為變化規律,將da/dN-ΔK關系曲線劃分為不同階段。原始材料da/dN-ΔK關系曲線的A'、B'階段分別為近門檻值階段和穩態裂紋擴展階段。在近門檻值階段,隨著ΔK的增加,da/dN呈快速上升趨勢。在穩態裂紋擴展階段,da/dN-ΔK關系曲線呈線性關系。服役材料的疲勞裂紋擴展行為較為復雜。其中,服役材料da/dN-ΔK關系曲線的A、B階段為近門檻值階段,C、D階段為穩態裂紋擴展階段。曲線擬合結果與前文穩態階段疲勞裂紋擴展行為一致,服役材料的擬合曲線在C、D階段呈折線形式。服役材料擬合曲線在A階段時,ΔK高于疲勞裂紋擴展門檻值(ΔKth),此時裂紋萌生并開始擴展,da/dN呈快速增長趨勢,可將此階段稱之為起始擴展階段。在曲線B階段,da/dN的增長趨勢減弱,曲線趨于平緩,這一階段服役材料的da/dN低于原始材料的基準水平(圖4中虛線部分),可將此階段稱之為延遲擴展階段。隨著ΔK的增加,da/dN再次呈快速上升趨勢(如服役材料曲線C階段所示),直至da/dN高于原始材料的基準水平,可將此階段稱之為快速擴展階段。da/dN在經歷C階段的快速上升后,進入D階段,即穩定擴展階段。服役材料D階段的疲勞裂紋擴展行為規律與原始材料差異較小。
圖4
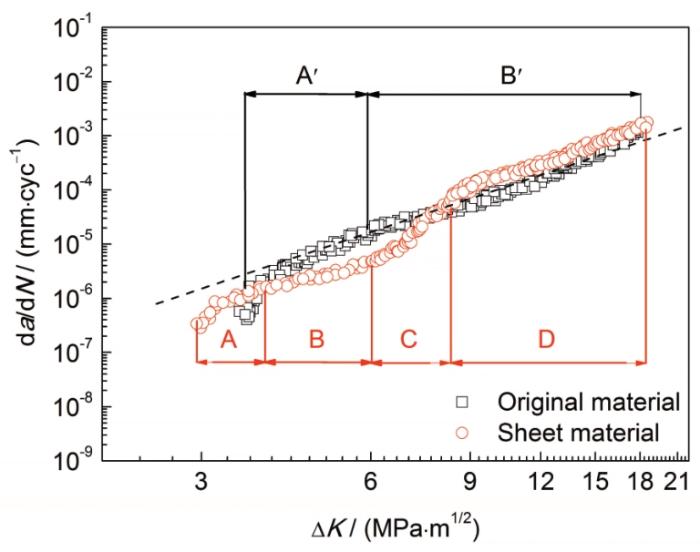
圖4 考慮近門檻值區域da/dN-ΔK關系曲線
Fig.4 da/dN-ΔK curves considering the range near fatigue crack propagation (FCP) threshold
綜上所述,服役材料的疲勞裂紋擴展行為較為復雜,即先后經歷起始擴展階段→延遲擴展階段→快速擴展階段→穩定擴展階段。由于長期經受外部環境的作用,環境介質以及循環載荷對材料疲勞裂紋擴展速率曲線中近門檻值階段和穩態裂紋擴展階段的行為規律有著顯著的影響。
3 分析討論
上文所述,經歷多年服役后,材料的疲勞裂紋擴展行為發生改變,即在穩態裂紋擴展階段發生折線現象。數據擬合結果表明,在疲勞裂紋擴展前期,裂紋擴展速率降低,材料斷裂力學性能提高。促使這一現象產生的因素有很多,如服役過程中經歷腐蝕、潮濕、溫度變化等復雜環境,同時受到不同循環載荷的作用也是重要的影響因素之一[25,26]。鑒于服役材料穩態裂紋擴展階段da/dN-ΔK關系的折線特征,通過施加預循環應力的方法來模擬高速列車結構材料的服役狀態,研究在不同水平的預循環應力作用后,疲勞裂紋擴展行為的變化規律。
3.1 預循環應力對材料疲勞裂紋擴展行為的影響
針對7N01鋁合金材料的標準三點彎曲試樣,進行不同水平預循環應力作用下的疲勞裂紋擴展實驗,研究材料在經歷預循環應力作用后,其疲勞裂紋擴展行為的變化規律。圖5為經歷預循環應力作用后,7N01鋁合金材料穩態裂紋擴展階段da/dN-ΔK的關系曲線。在預循環應力的作用下,其穩態裂紋擴展階段的疲勞裂紋擴展速率均低于初始狀態材料,反映出此階段材料抵抗裂紋擴展的能力整體提高,施加預循環應力促使材料產生“鍛煉”效應。“鍛煉”效應是金屬材料疲勞過程中的一個有趣現象。一方面,經歷低于疲勞極限的預循環應力作用會對材料造成一定程度的損傷,產生表面裂紋;但另一方面,預循環應力能夠促使材料的疲勞強度和斷裂性能有所提高[18]。施加預循環應力是材料產生“鍛煉”效應的原因,“鍛煉”效應與預循環應力水平有關[27],不同水平的預循環應力促使材料產生的“鍛煉”效果不盡相同。從圖5可見,疲勞裂紋擴展速率隨著預循環應力水平的增加而先減慢后加快,說明存在能夠使材料達到最佳“鍛煉”效果的預循環應力水平。在達到最佳“鍛煉”效果之前,預循環應力水平逐漸增加可以視為材料產生強化的過程;達到最佳預循環應力水平時,材料的“鍛煉”效果最為明顯;當超過最佳預循環應力水平后,強化效果逐漸減小并開始對材料產生損傷,材料的“鍛煉”效果也隨之逐漸減小直至消失。在本工作給定的預循環應力水平中,強化效果較為明顯的預循環應力范圍為30~60 MPa,即疲勞極限的19%~38%范圍內。
圖5
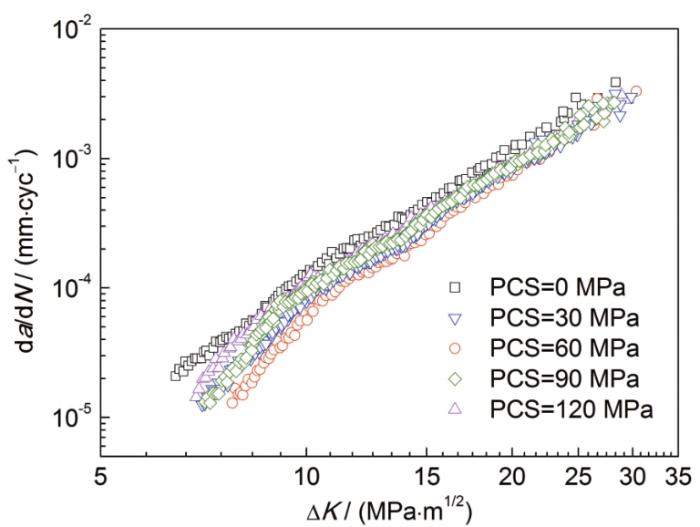
圖5 預循環應力作用后穩態裂紋擴展階段da/dN-ΔK關系曲線
Fig.5 da/dN-ΔK curves in the steady growth zone subjected to pre-cyclic stress (PCS)
圖6給出不同ΔK所對應的da/dN。選取ΔK=8、15、20和25 MPa·m1/2來觀測不同水平預循環應力對da/dN影響的變化規律。由圖6可見,在選取的4個ΔK下,da/dN隨預循環應力水平的增加而先減慢后加快。在同一ΔK下,預循環應力為60 MPa時,其da/dN最低。相對于初始狀態材料,ΔK=8、15、20和25 MPa·m1/2時,其da/dN分別降低了66.4%、41.9%、37.2%和33.9%。
圖6
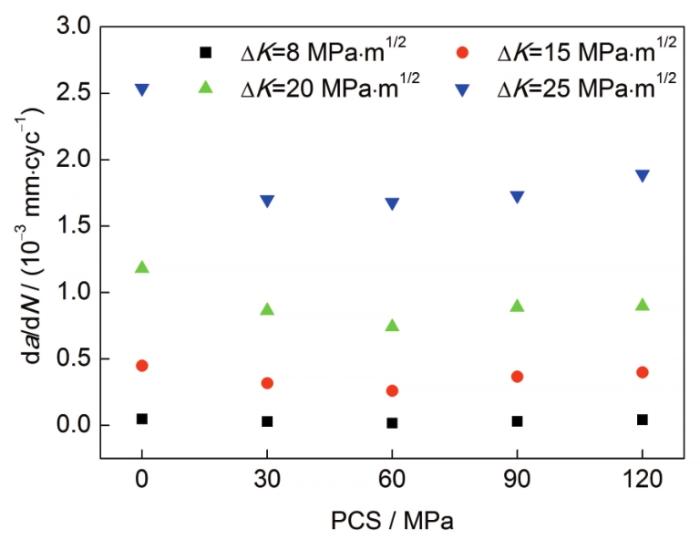
圖6 不同應力強度因子范圍所對應的疲勞裂紋擴展速率
Fig.6 The increase of da/dN with different PCSs at different ΔK
不同應力強度因子范圍所對應的疲勞裂紋擴展速率的變化規律結果表明,預循環應力促使材料產生的“鍛煉”效應對穩態裂紋擴展的各個階段影響程度不盡相同。其中,在低應力強度因子范圍內,疲勞裂紋擴展速率降低幅度最為明顯,預循環應力的“鍛煉”作用最為顯著。與服役材料的疲勞裂紋擴展行為規律相似,預循環應力促使材料穩態裂紋擴展初期階段的疲勞裂紋擴展行為表現為折轉形式。在產生折轉現象之前,疲勞裂紋擴展速率對應力強度因子較為敏感,呈現快速上升趨勢。經過轉折點后,材料的疲勞裂紋擴展行為相對穩定,與初始狀態材料的da/dN-ΔK關系曲線呈現平行擴展模式,且不同預循環應力水平的da/dN-ΔK關系曲線較為接近。
綜上所述,根據服役材料和經歷預循環應力作用材料的穩態裂紋擴展階段da/dN-ΔK關系曲線可知,二者在穩態裂紋擴展初期階段均呈現折線特征。服役材料da/dN-ΔK關系曲線的折線現象更為顯著,形成2條斜率明顯不同的曲線。預循環應力促使材料穩態裂紋擴展階段的疲勞裂紋擴展速率整體降低,而服役經歷對材料疲勞裂紋擴展行為的影響主要體現在穩態裂紋擴展初期階段。這是由于材料在服役過程中,受到復雜環境因素的影響,降低材料穩態裂紋擴展初期的疲勞裂紋擴展速率,從而影響其疲勞裂紋擴展行為。隨著裂紋不斷擴展,力學因素成為影響疲勞裂紋擴展速率的主要因素,此時服役材料的疲勞裂紋擴展行為規律與原始材料相似。預循環應力對材料的“鍛煉”效應也可以解釋服役材料穩態裂紋擴展初期階段斷裂力學性能提高的原因,即在長期的服役過程中,高速列車結構材料經受各種低幅循環載荷的作用,這些低幅循環載荷可能促使材料產生強化作用,抵抗裂紋萌生和啟裂的能力增強。
3.2 預循環應力對材料疲勞裂紋擴展壽命的影響
針對不同水平預循環應力作用下的疲勞裂紋擴展實驗數據進行線性回歸分析。應用Paris公式,通過最小二乘法原理擬合得到da/dN與ΔK的理論Paris曲線。
圖7給出7N01鋁合金材料的理論Paris曲線擬合結果。與服役材料擬合結果相似,由于預循環應力作用的影響,實驗數據點未能與理論Paris曲線相吻合。鑒于其曲線表現為折線形式,以折線現象的轉折點作為整體擬合曲線的分隔點,采用分階段的方式對服役材料da/dN-ΔK關系曲線進行分析。為了清晰呈現分段擬合的方法,以預循環應力為0和60 MPa的實驗數據為例,分段擬合示意圖如圖8所示。同時,確定產生折轉現象轉折點所對應的ΔK,對發生折轉前后的2段曲線分別進行擬合處理,獲得各階段da/dN-ΔK關系曲線的材料常數lgC和m。由于初始狀態材料試樣未發生明顯的折轉現象,da/dN-ΔK關系曲線呈現線性關系,故認為其分段前后的材料常數一致。表1給出材料在不同水平預循環應力作用下,轉折點處所對應的ΔK以及Paris公式分段擬合后的材料常數。可見,在預循環應力作用下,前段Paris曲線(曲線1)相對于后段Paris曲線(曲線2),其斜率m增大,截距lgC減小。轉折點處對應的ΔK隨給定預循環應力水平的增大而先增大后減小。
圖7
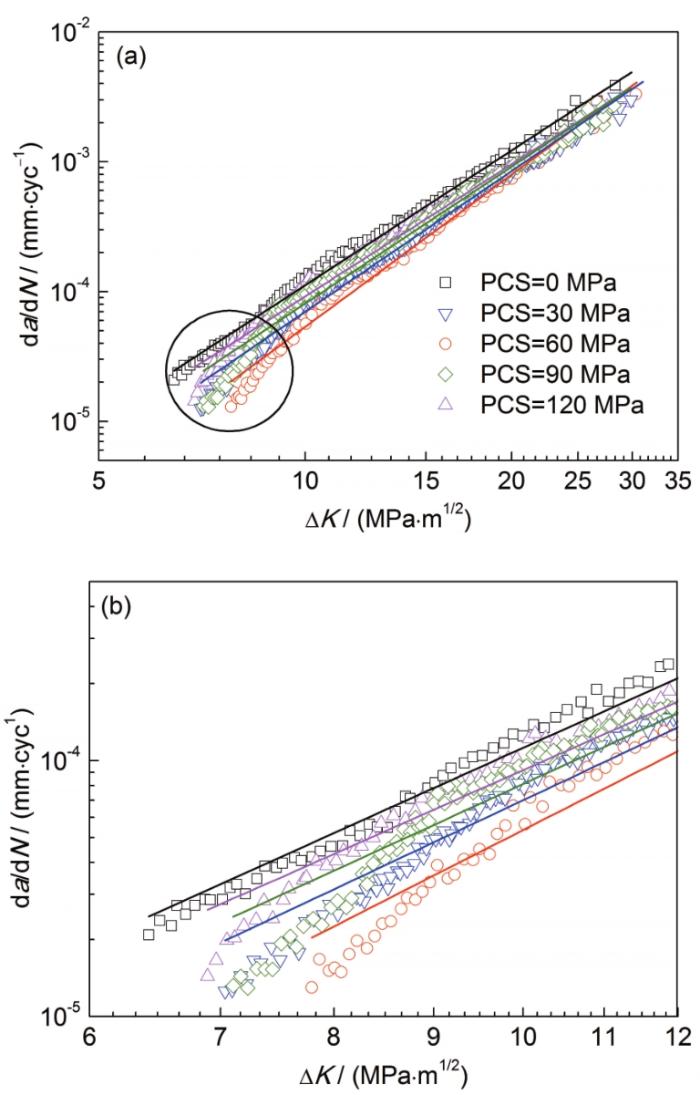
圖7 疲勞裂紋擴展實驗數據與理論Paris曲線結果
Fig.7 Experimental data and the Paris fitted curves (a) and drawing of partial enlargement (b)
圖8

圖8 分段擬合示意圖
Fig.8 Fitted curves of the experimental data-piecewise curve fitting
表1 Paris公式分段擬合得到的材料常數
Table 1
|
PCS MPa |
ΔK at the turning point MPa·m1/2 |
Whole fitting | Piecewise fitting (curve 1) | Piecewise fitting (curve 2) | |||
|---|---|---|---|---|---|---|---|
| lgC | m | lgC | m | lgC | m | ||
| 0 | - | -7.39186 | 3.44199 | -7.39186 | 3.44199 | -7.39186 | 3.44199 |
| 30 | 10.41 | -7.75152 | 3.59695 | -9.41163 | 5.33065 | -7.52036 | 3.41039 |
| 60 | 11.55 | -8.16278 | 3.89175 | -9.95825 | 5.72909 | -7.79621 | 3.60007 |
| 90 | 10.81 | -7.58924 | 3.49789 | -9.77501 | 5.77199 | -7.30743 | 3.27054 |
| 120 | 10.22 | -7.41945 | 3.38241 | -8.92749 | 5.00362 | -7.12119 | 3.14091 |
經歷預循環應力作用后,材料的疲勞裂紋擴展行為發生改變,應用整體Paris曲線計算出的材料常數C和m來預測其疲勞裂紋擴展壽命并不準確。因此,在預測疲勞裂紋擴展壽命過程中,應該根據擬合曲線的疲勞裂紋擴展行為特性進行考慮。
將Paris公式進行積分處理,可得到整體擬合曲線的疲勞裂紋擴展壽命估算公式為:
根據轉折點處所對應的裂紋擴展長度,將整體擬合曲線劃分為2個部分,分段擬合方法的疲勞裂紋擴展壽命估算公式為:
式中,NP為疲勞裂紋擴展壽命;N0和Nf分別為疲勞裂紋擴展初始壽命和最終壽命;a0為試樣切口長度與預制疲勞裂紋長度之和;ac為試樣斷裂時的裂紋擴展長度;ai為轉折點處所對應的裂紋擴展長度;C1、m1和C2、m2分別為分段擬合的材料常數。
根據式(5)和(6)分別計算獲得7N01鋁合金材料在不同水平預循環應力作用下,其整體擬合曲線和分段擬合曲線的疲勞裂紋擴展壽命預測結果,并與疲勞裂紋擴展實驗實測數據進行比較。圖9給出7N01鋁合金材料疲勞裂紋擴展壽命預測結果的對比圖。可以看出,由于經歷預循環應力作用,材料的疲勞裂紋擴展壽命均有不同程度提高。預循環應力對材料疲勞裂紋擴展壽命的影響規律與其疲勞裂紋擴展行為規律一致,即疲勞裂紋擴展壽命隨預循環應力水平的增加而先增大后減小。相對于初始狀態材料,在預循環應力為30、60、90和120 MPa時,疲勞裂紋擴展壽命預測結果分別提高了15.9%、24.1%、13.2%和12.1%。
圖9
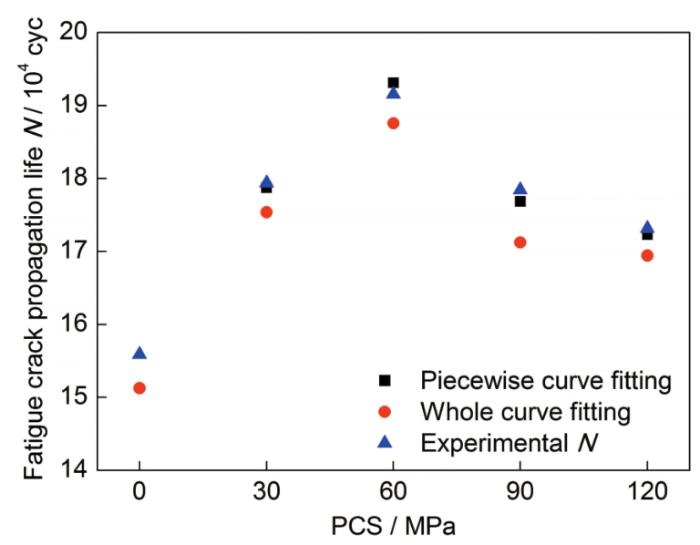
圖9 疲勞裂紋擴展壽命預測結果對比圖
Fig.9 PCS life prediction based on whole curve fitting and piecewise curve fitting
從圖9中分段擬合曲線的疲勞裂紋擴展壽命預測結果可以看出,其結果均高于整體擬合曲線的疲勞裂紋擴展壽命預測值。相對于整體擬合曲線預測結果,在預循環應力為30、60、90和120 MPa時,分段擬合方法獲得的疲勞裂紋擴展壽命分別提高了1.9%、2.9%、3.3%和1.7%。
將2種擬合曲線方法獲得的疲勞裂紋擴展壽命與實驗數據進行比較可以看出,分段擬合方法的預測結果與實驗數據更為接近。這證明整體曲線擬合方法的預測結果并不適用于對經歷預循環應力作用后的材料進行疲勞裂紋擴展壽命預測,而本工作提出的疲勞裂紋擴展壽命計算模型能夠更加準確地預測預循環應力作用下的材料疲勞裂紋擴展壽命。
4 結論
(1) 服役經歷促使材料的疲勞裂紋擴展行為發生改變,即穩態裂紋擴展階段da/dN-ΔK關系表現為折線形式,在低應力強度因子范圍內,疲勞裂紋擴展速率呈現快速上升的趨勢,經過轉折點處后,擴展行為趨于穩定。
(2) 服役材料的疲勞裂紋擴展行為較為復雜,即先后經歷起始擴展階段→延遲擴展階段→快速擴展階段→穩定擴展階段。服役環境對材料近門檻值階段和穩態裂紋擴展初期階段的擴展行為有著顯著的影響,近門檻值區域的延遲擴展是促使服役材料da/dN-ΔK關系呈折線形式的原因。
(3) 鑒于服役材料穩態裂紋擴展階段的折線特征,設計基于預循環應力作用的斷裂力學性能實驗測試方案。預循環應力促使材料產生“鍛煉”效應,不同預循環應力水平對材料結構強度的“鍛煉”效果不同,存在能夠使材料達到最佳“鍛煉”效果的預循環應力范圍。在本工作給定的預循環應力水平中,“鍛煉”效果較為明顯的預循環應力水平范圍為30~60 MPa,即材料疲勞極限的19%~38%。
(4) 根據服役材料和經歷預循環應力作用材料的疲勞裂紋擴展行為特性,提出分段擬合的描述方法并建立疲勞裂紋擴展壽命預測模型,對于折轉型da/dN-ΔK關系曲線,該計算模型能夠更加準確地預測材料的疲勞裂紋擴展壽命
來源--金屬學報







 滬公網安備31011202020290號
滬公網安備31011202020290號
