郭東偉1,2, 郭坤輝1,2, 張福利1,2, 張飛1,2, 曹江海1,2, 侯自兵,1,2

連鑄坯內(nèi)部中心偏析缺陷的存在會(huì)對(duì)鑄坯以及后續(xù)產(chǎn)品質(zhì)量和性能產(chǎn)生影響[1~3],而中心偏析的形成與鑄坯內(nèi)部凝固組織特征密切相關(guān)。現(xiàn)有研究[4~7]表明,鑄坯內(nèi)部發(fā)達(dá)的柱狀晶會(huì)導(dǎo)致較為嚴(yán)重的中心線偏析,而擴(kuò)大鑄坯中心等軸晶區(qū)有利于減輕中心偏析缺陷。因此,針對(duì)鑄坯內(nèi)部柱狀晶向等軸晶轉(zhuǎn)變(columnar to equiaxed transition,CET)的判斷對(duì)于控制鑄坯內(nèi)部凝固組織,提高鑄坯質(zhì)量具有重要意義。

近年來(lái),學(xué)者們針對(duì)合金內(nèi)部CET判斷進(jìn)行了相關(guān)研究,提出了不同的CET判定方法。Hunt[8]提出了第一個(gè)確定性的CET判斷模型并分析了合金成分、形核密度以及過(guò)冷度對(duì)CET的影響,認(rèn)為當(dāng)柱狀晶前沿等軸晶粒體積分?jǐn)?shù)達(dá)到0.49時(shí)即發(fā)生CET。在此基礎(chǔ)之上,Shibata等[9]對(duì)Hunt[8]模型進(jìn)行改進(jìn),提出了針對(duì)不銹鋼連鑄板坯等軸晶率預(yù)測(cè)的簡(jiǎn)化模型并探究了拉速、過(guò)熱度等對(duì)板坯內(nèi)部等軸晶率的影響。Niu等[10]對(duì)Hunt[8]模型進(jìn)行了修正,針對(duì)38CrMoAl圓坯提出了結(jié)合CET判定、傳熱數(shù)值模擬以及數(shù)據(jù)檢測(cè)的預(yù)測(cè)模型,該模型可以避免異質(zhì)形核密度的不正確選擇。然而,目前針對(duì)碳鋼連鑄坯內(nèi)部CET判定模型的研究仍較少,且現(xiàn)有模型多是基于凝固過(guò)程參數(shù)的復(fù)雜計(jì)算并側(cè)重于對(duì)鑄坯整體CET位置進(jìn)行判斷,忽略了對(duì)于鑄坯內(nèi)部實(shí)際凝固組織的觀察和表征以及實(shí)際凝固組織所具有的波動(dòng)性。與此同時(shí),隨著數(shù)學(xué)模型和計(jì)算機(jī)技術(shù)的進(jìn)步,合金內(nèi)部微觀結(jié)構(gòu)形態(tài)的模擬得到發(fā)展。Luo等[11]通過(guò)耦合元胞自動(dòng)機(jī)有限差分(cellular automaton-finite difference,CA-FD)模型對(duì)連鑄鋼坯內(nèi)部凝固過(guò)程以及枝晶生長(zhǎng)過(guò)程進(jìn)行模擬,再現(xiàn)了連鑄過(guò)程鑄坯內(nèi)部枝晶競(jìng)爭(zhēng)生長(zhǎng)和CET轉(zhuǎn)變,并探究了過(guò)熱度對(duì)于鑄坯等軸晶率的影響。Hou等[12]建立了元胞自動(dòng)機(jī)有限元(cellular automaton-finite element,CAFE)耦合模型,分析了高碳鋼連鑄坯內(nèi)部凝固組織演變以及中心等軸晶區(qū)晶粒致密度,并探究了過(guò)熱度和連鑄拉速對(duì)鑄坯等軸晶率的影響。鑄坯內(nèi)部微觀結(jié)構(gòu)形態(tài)的模擬可以對(duì)枝晶生長(zhǎng)和等軸晶區(qū)分布進(jìn)行反映,從而對(duì)比不同工藝下的凝固組織特征情況,但是針對(duì)實(shí)際鑄坯內(nèi)部CET位置的判斷仍缺乏統(tǒng)一有效的定量標(biāo)準(zhǔn)。另一方面,在實(shí)際連鑄現(xiàn)場(chǎng)生產(chǎn)過(guò)程中多采用低倍檢驗(yàn)的方法對(duì)鑄坯質(zhì)量進(jìn)行判斷,并通過(guò)鑄坯實(shí)際凝固組織特征對(duì)等軸晶區(qū)域進(jìn)行定性的判定；但是由于鑄坯CET位置附近枝晶形貌較為復(fù)雜,其判定結(jié)果往往存在偏差。針對(duì)合金實(shí)際凝固組織,亦有學(xué)者[13~15]基于凝固組織的不同形態(tài),采用合金內(nèi)部晶粒縱橫比來(lái)對(duì)合金內(nèi)部CET位置進(jìn)行判斷。然而,碳鋼內(nèi)部凝固組織形態(tài)較為復(fù)雜,枝晶熔斷、黏合現(xiàn)象較為普遍,晶粒縱橫比的測(cè)量較為困難。因此,一種能夠基于實(shí)際連鑄坯復(fù)雜凝固組織對(duì)CET起始位置進(jìn)行定量判斷的方法,對(duì)于實(shí)際生產(chǎn)中指導(dǎo)生產(chǎn)工藝,提高鑄坯質(zhì)量非常重要。

基于以上背景,本工作以SCM440冷鐓鋼連鑄坯為研究對(duì)象,從連鑄坯實(shí)際凝固組織入手對(duì)鑄坯內(nèi)部二次枝晶間距(secondary dendrite arm spacing,SDAS)變化進(jìn)行測(cè)量分析,同時(shí),結(jié)合鑄坯橫斷面二維溫度場(chǎng)模型分析鑄坯由表面至中心傳熱條件的變化并探究SDAS的變化原因。在此基礎(chǔ)之上,提出了基于鑄坯內(nèi)部SDAS變化特征的連鑄坯CET定量判斷新方法,該方法可為實(shí)際連鑄坯CET判斷以及生產(chǎn)工藝調(diào)控提供方法和理論指導(dǎo)。

1 實(shí)驗(yàn)方法與溫度場(chǎng)模擬

1.1 實(shí)驗(yàn)材料

采用尺寸為160 mm × 160 mm的SCM440冷鐓鋼為研究對(duì)象,其主要成分(質(zhì)量分?jǐn)?shù),%)為：C 0.38~0.43,Si 0.15~0.3,Mn 0.60~0.90,P ≤ 0.002,S ≤ 0.002,Cr 0.90~1.20,Mo 0.15~0.30,Fe余量。按照圖1所示方式在現(xiàn)場(chǎng)正常生產(chǎn)條件下取得2塊連鑄坯橫斷面試樣,試樣生產(chǎn)工藝如表1所示。由于澆鑄過(guò)程中鋼包鋼水溫度降低,需提高連鑄拉速,因此2塊試樣工藝參數(shù)的主要區(qū)別在于過(guò)熱度和拉速。No.1試樣過(guò)熱度較高,拉速偏低；No.2試樣過(guò)熱度較低,拉速偏高。同時(shí),連鑄過(guò)程中在鑄機(jī)結(jié)晶器和二冷四區(qū)之后凝固末端分別施加電磁攪拌(參數(shù)分別為330 A、6 Hz和690 A、50 Hz)。在得到實(shí)際鑄坯橫斷面試樣之后,為獲得連鑄坯橫斷面凝固組織特征,采用國(guó)家標(biāo)準(zhǔn)(GB/T 226-2015)對(duì)2塊試樣進(jìn)行熱酸洗實(shí)驗(yàn)。熱酸洗實(shí)驗(yàn)中酸液為HCl溶液(分析純)∶H2O = 1∶1 (體積比)的溶液,酸蝕溫度為60~80℃,酸蝕時(shí)間為15~20 min[16,17]。熱酸洗實(shí)驗(yàn)之后在相同光源條件下使用SONY $?$6000數(shù)碼相機(jī)采集2塊試樣低倍組織圖像。

圖1

圖1   連鑄坯橫斷面取樣方法示意圖

Fig.1   Schematic of sampling method for cross section of the selected continuous casting billets

表1   SCM440連鑄方坯主要生產(chǎn)工藝參數(shù)

Table 1  Production parameters of selected SCM440 continuous casting billet

新窗口打開(kāi)| 下載CSV

1.2 凝固組織SDAS測(cè)量

獲得低倍組織圖像后,按照圖2所示,在2塊試樣橫斷面左右側(cè)分別取中心線、近內(nèi)弧側(cè)(距離中心線15 mm)和近外弧側(cè)(距離中心線15 mm) 3個(gè)位置。每個(gè)位置處由鑄坯表面至中心依次選取典型樹(shù)枝晶,利用Image-Pro Plus 6.0軟件采用截線法對(duì)所選典型枝晶SDAS進(jìn)行測(cè)量,同時(shí)記錄每個(gè)SDAS測(cè)量位置與鑄坯表面之間的距離。

圖2

圖2   連鑄坯試樣橫斷面二次枝晶間距(SDAS)測(cè)量位置

Fig.2   Schematic of measurement position of secondary dendrite arm spacing (SDAS) in cross section of selected continuous casting billets

1.3 二維溫度場(chǎng)模擬及驗(yàn)證

連鑄過(guò)程中,鑄坯內(nèi)部凝固組織的形成與凝固過(guò)程的傳熱過(guò)程以及鑄坯內(nèi)部溫度分布密切相關(guān)。本工作目的旨在能夠基于連鑄坯內(nèi)部SDAS變化特征對(duì)鑄坯內(nèi)部CET位置進(jìn)行定量判斷,為了對(duì)研究結(jié)果進(jìn)行驗(yàn)證與反映,利用ANSYS 2020R1 軟件對(duì)2塊鑄坯橫斷面二維溫度場(chǎng)進(jìn)行計(jì)算模擬。

1.3.1 傳熱方程

本工作中鑄坯試樣凝固過(guò)程的傳熱計(jì)算基于有限元理論,計(jì)算過(guò)程中的二維傳熱方程為[18]：

式中,λ為熱導(dǎo)率,W/(m·℃)； $?$為鋼液密度,kg/m3；cp 為定壓比熱容,J/(kg·℃)；T為溫度,℃；t為時(shí)間,s；x、y分別是水平方向和縱向的長(zhǎng)度,m。實(shí)際鑄坯連鑄過(guò)程中施加了結(jié)晶器及末端電磁攪拌對(duì)內(nèi)部質(zhì)量進(jìn)行控制,因此在二維溫度場(chǎng)模型計(jì)算過(guò)程中,通過(guò)λ的變化來(lái)反映電磁場(chǎng)對(duì)鑄坯內(nèi)部傳熱的影響。二維溫度場(chǎng)計(jì)算過(guò)程中,連鑄坯拉坯方向的傳熱忽略不計(jì)。使用有效比熱法將凝固過(guò)程中潛熱的演變納入計(jì)算之中[18]：

式中, ${?}_{?}^{\text{'}}$為有效比熱容,J/(kg·℃)；L為潛熱,J/kg；fs為固相體積分?jǐn)?shù)。

1.3.2 邊界條件與初始條件

本工作建立了基于切片運(yùn)動(dòng)的非穩(wěn)態(tài)傳熱模型來(lái)模擬鑄坯橫斷面二維溫度場(chǎng),模型中單個(gè)網(wǎng)格的尺寸為3 mm × 3 mm。計(jì)算過(guò)程中假設(shè)鑄坯切片由連鑄結(jié)晶器經(jīng)足輥區(qū)運(yùn)動(dòng)至二冷區(qū),最終經(jīng)切割點(diǎn)運(yùn)動(dòng)至上冷床階段。切片的尺寸與實(shí)際連鑄坯試樣尺寸相同,即160 mm × 160 mm,切片厚度為30 mm。假設(shè)切片垂直于拉坯方向的2個(gè)面是絕熱的,隨著連鑄凝固過(guò)程的進(jìn)行,改變切片其他4個(gè)面的傳熱條件來(lái)模擬試樣的實(shí)際連鑄過(guò)程。結(jié)晶器、足輥區(qū)、二冷區(qū)以及空冷區(qū)的長(zhǎng)度、邊界條件以及相應(yīng)參數(shù)計(jì)算公式如表2[18~20]所示。其中,qm、qf、qk和qa分別為結(jié)晶器、足輥區(qū)、二冷區(qū)以及空冷區(qū)的熱通量,kW/m2；tm為切片處于結(jié)晶器中的時(shí)間,s；β為關(guān)于結(jié)晶器形狀以及連鑄參數(shù)的系數(shù),kW/(m2·s1/2)；hf和hk為足輥區(qū)和二冷區(qū)的傳熱系數(shù),W/(m2·℃)；w為冷卻水流量,L/(m2·min)； $?$為輻射傳熱系數(shù)； $?$為Stefan-Boltzmann 常數(shù)；Tb、Tf、Tw和Ta分別為鑄坯表面溫度、足輥區(qū)水流溫度、二冷區(qū)水流溫度以及空冷區(qū)環(huán)境溫度,℃。計(jì)算的初始條件為[18]：

表2   溫度場(chǎng)計(jì)算過(guò)程中各部分參數(shù)及計(jì)算公式[18~20]

Table 2  Parameters and relevant computational formulas at different sections in the calculation of temperature field[18-20]

新窗口打開(kāi)| 下載CSV

式中,Tcast為鋼包內(nèi)鋼水溫度,℃。

1.3.3 模型驗(yàn)證

為了使模型更為準(zhǔn)確地反映連鑄坯凝固過(guò)程中的傳熱過(guò)程及鑄坯內(nèi)部溫度分布,進(jìn)而對(duì)其實(shí)際凝固組織進(jìn)行分析,需對(duì)所建立的二維溫度場(chǎng)模型進(jìn)行驗(yàn)證。由于碳鋼連鑄坯內(nèi)部實(shí)際凝固組織較為復(fù)雜,用二維溫度場(chǎng)模型較難對(duì)其進(jìn)行反映,同時(shí),本工作主要利用橫斷面各點(diǎn)的溫度及溫度梯度變化對(duì)鑄坯內(nèi)部傳熱過(guò)程進(jìn)行反映,因此,決定采用實(shí)際連鑄坯表面中心溫度與數(shù)值模擬溫度對(duì)比的方式對(duì)模型準(zhǔn)確性進(jìn)行驗(yàn)證。在No.1鑄坯現(xiàn)場(chǎng)生產(chǎn)過(guò)程中,在彎月面至鑄坯上冷床冷卻之間選取4個(gè)位置點(diǎn),對(duì)4個(gè)位置點(diǎn)處鑄坯右側(cè)表面中心溫度進(jìn)行測(cè)量,并將其與數(shù)值計(jì)算結(jié)果進(jìn)行對(duì)比,結(jié)果如表3所示。分析結(jié)果可知,鑄坯表面的實(shí)際溫度與數(shù)值模擬結(jié)果之差均在30℃以內(nèi),表明所建立的溫度場(chǎng)模型是有效的,可以基于此溫度場(chǎng)模型來(lái)研究實(shí)際鑄坯凝固過(guò)程溫度場(chǎng)的變化。

表3   No.1鑄坯右側(cè)表面中心測(cè)溫結(jié)果與溫度場(chǎng)數(shù)值模擬結(jié)果對(duì)比

Table 3  Comparison of temperature measurement results and numerical simulation results of temperature field at the center of right surface of billet No.1

新窗口打開(kāi)| 下載CSV

2 結(jié)果與討論

2.1 鑄坯橫斷面低倍組織及SDAS變化

圖3為測(cè)量所得No.1和No.2鑄坯橫斷面左右側(cè)各位置處的SDAS變化。由圖可知,鑄坯中心SDAS整體大于邊部,該過(guò)程主要體現(xiàn)鑄坯凝固組織由外部較為細(xì)密的柱狀晶轉(zhuǎn)變?yōu)橹行妮^為粗大的等軸晶。同時(shí),觀察發(fā)現(xiàn),在2塊試樣所有選定位置處SDAS的測(cè)量過(guò)程中均存在某一位置(圖3中箭頭所指),該位置存在SDAS較大幅度的突變并伴隨著SDAS的最大增加率。李博等[21]在高強(qiáng)石油套管鋼內(nèi)部點(diǎn)狀偏析研究過(guò)程中對(duì)鋼坯由表面至中心的SDAS進(jìn)行了測(cè)量,發(fā)現(xiàn)在CET位置處SDAS有較大的增加速率,但SDAS突增的原因以及其與CET之間的聯(lián)系并未詳細(xì)給出。Ji等[22]研究了高碳鋼內(nèi)部枝晶形貌及中心偏析對(duì)后續(xù)熱軋線材組織和力學(xué)性能的影響,在對(duì)高碳鋼連鑄方坯內(nèi)部SDAS測(cè)量過(guò)程中也存在CET位置處的SDAS突增,但也未深入探究其與CET之間的聯(lián)系。連鑄坯內(nèi)部SDAS可表示為[22]：

圖3

圖3   No.1和No.2鑄坯橫斷面左右側(cè)各位置的SDAS變化

Fig.3   SDAS changes on the cross section of the billets No.1 (a, c, e) and No.2 (b, d, f)

(a, b) near inner arc side (c, d) centerline (e, f) near outer arc side

式中,dS為鑄坯內(nèi)部二次枝晶間距,mm；G為鑄坯凝固前沿溫度梯度,℃/mm；v為鑄坯凝固過(guò)程中的枝晶生長(zhǎng)速率,mm/min；θ和α均為擬合系數(shù)。

由 式(4)可知,鑄坯內(nèi)部SDAS與凝固過(guò)程中鑄坯內(nèi)部溫度梯度及凝固組織生長(zhǎng)速率有關(guān),而溫度梯度和生長(zhǎng)速率與鑄坯內(nèi)部傳熱密切相關(guān)。結(jié)合前人研究[21,22]以及本工作中實(shí)際SDAS測(cè)量結(jié)果,推測(cè)在凝固過(guò)程中由鑄坯表面至中心凝固組織的變化導(dǎo)致傳熱條件發(fā)生了較為劇烈的變化,而這種變化最終以枝晶形貌的形式表現(xiàn)出來(lái)。鑄坯表面至中心凝固組織主要為表層激冷層、柱狀晶區(qū)以及中心等軸晶區(qū)。柱狀晶具有各向異性的特點(diǎn),當(dāng)其穩(wěn)定生長(zhǎng)時(shí),熱流沿柱狀晶生長(zhǎng)方向近似垂直于鑄坯表面向外傳遞。等軸晶具有各向同性的特點(diǎn),在等軸晶形核長(zhǎng)大的過(guò)程中熱量向各個(gè)方向進(jìn)行傳遞。柱狀晶向等軸晶轉(zhuǎn)變的過(guò)程中,由于2者傳熱特點(diǎn)的差異性,可能導(dǎo)致鑄坯內(nèi)部SDAS的變化。基于此,針對(duì)鑄坯由表面至中心SDAS以及傳熱過(guò)程的變化進(jìn)行研究,以探究鑄坯內(nèi)部凝固組織特征與CET之間的關(guān)系。

2.2 鑄坯橫斷面溫度梯度與生長(zhǎng)速率變化

2.2.1 溫度梯度

圖4為基于二維溫度場(chǎng)模型得到的2塊鑄坯試樣橫斷面左側(cè)中心線位置處由表面至中心的溫度梯度變化,此過(guò)程中計(jì)算所得溫度梯度為鑄坯由中心至表面方向溫度梯度的矢量和。在實(shí)際凝固組織特征的分析過(guò)程中,本工作針對(duì)橫斷面左右側(cè)分別選取了3個(gè)分析位置,即中心線、近內(nèi)弧側(cè)以及近外弧側(cè)。在后續(xù)溫度場(chǎng)數(shù)據(jù)的分析過(guò)程中,3個(gè)位置的溫度場(chǎng)數(shù)據(jù)雖存在差異但不明顯,因此,采用橫斷面左側(cè)中心線的溫度場(chǎng)數(shù)據(jù)作為代表,分析其與實(shí)際凝固組織特征變化之間的聯(lián)系。觀察圖4可知,2塊鑄坯由表面至中心溫度梯度變化均可大致分為3段。其中,A段為初始凝固階段,在這一過(guò)程中,鋼液通過(guò)浸入式水口進(jìn)入結(jié)晶器接觸水冷銅壁冷卻,溫度梯度迅速增加至較大值。隨著凝固進(jìn)行,凝固坯殼厚度逐漸增大,熱阻也逐漸增加,鑄坯內(nèi)部溫度梯度快速下降。連鑄坯結(jié)晶器內(nèi)初始凝固階段的凝固組織主要為激冷層細(xì)小等軸晶以及初始柱狀晶,與后續(xù)CET關(guān)聯(lián)較小。因此,針對(duì)鑄坯內(nèi)部溫度梯度變化,著重對(duì)B和C 2段進(jìn)行分析。

圖4

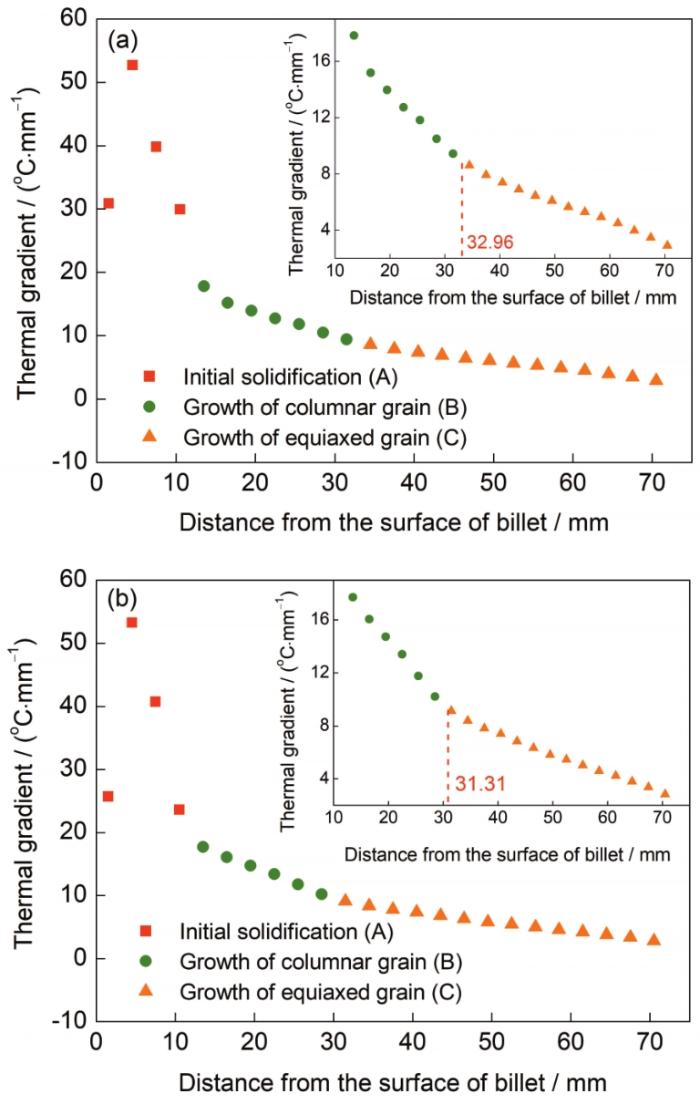
圖4   No.1和No.2鑄坯左側(cè)中心線處的溫度梯度變化

Fig.4   Thermal gradient changes on the left centerline of billets No.1 (a) and No.2 (b) (Insets show the high magnified images)

由圖4局部放大圖可知,B和C段溫度梯度整體上存在減小的趨勢(shì),但2段過(guò)程中溫度梯度的減小速率不同,B段溫度梯度減小速率較快,C段溫度梯度減小速率較慢,這與2段過(guò)程所對(duì)應(yīng)的凝固組織特征有關(guān)。在鑄坯由外向內(nèi)凝固過(guò)程中,B段為柱狀晶穩(wěn)定生長(zhǎng)階段,此時(shí)鑄坯內(nèi)部熱量以近似一維傳熱的形式向外較快傳遞,溫度梯度較大,在此情況下,柱狀晶快速生長(zhǎng),傳熱熱阻逐漸增大,因此溫度梯度減小速率也較快。C段為等軸晶生長(zhǎng)階段,此時(shí),晶粒的各向同性使得一維傳熱被阻斷,熱量由內(nèi)向外傳輸?shù)男式档?因此溫度梯度減小速率減慢。總體而言,在鑄坯由外向內(nèi)凝固的過(guò)程中,伴隨著柱狀晶向等軸晶的轉(zhuǎn)變,溫度梯度的變化趨勢(shì)也會(huì)隨之發(fā)生改變,在溫度梯度變化的拐點(diǎn)處則意味著柱狀晶向等軸晶的轉(zhuǎn)變點(diǎn),即CET位置。對(duì)B和C段溫度梯度變化曲線進(jìn)行擬合并計(jì)算出拐點(diǎn)所在位置,可知2塊鑄坯試樣內(nèi)部溫度梯度變化分別在距鑄坯表面32.96和31.31 mm處發(fā)生轉(zhuǎn)變,即No.1和No.2鑄坯分別在距離鑄坯表面32.96和31.31 mm的位置處發(fā)生CET。

2.2.2 生長(zhǎng)速率

鑄坯內(nèi)部SDAS除與溫度梯度有關(guān),還受生長(zhǎng)速率的影響,為了更為詳細(xì)系統(tǒng)地探究鑄坯內(nèi)部凝固組織及傳熱條件的變化,基于本研究所選連鑄坯二維溫度場(chǎng)模型對(duì)橫斷面左側(cè)中心線上枝晶生長(zhǎng)速率進(jìn)行計(jì)算,結(jié)果如圖5所示。由于數(shù)值計(jì)算過(guò)程中實(shí)際枝晶的生長(zhǎng)難以觀測(cè),本工作利用中心線上相鄰網(wǎng)格達(dá)到鋼液固相線的時(shí)間差來(lái)計(jì)算鑄坯內(nèi)部枝晶生長(zhǎng)速率。由圖5可知,生長(zhǎng)速率變化的過(guò)程中,在D段出現(xiàn)短暫的降低,其后E和G段整體呈現(xiàn)逐漸增加的趨勢(shì),僅在過(guò)程中間F段存在生長(zhǎng)速率的短時(shí)間內(nèi)突降。結(jié)合之前分析可知,D段對(duì)應(yīng)鋼液在結(jié)晶器內(nèi)的初始凝固狀態(tài)。鋼液剛進(jìn)入結(jié)晶器時(shí)接觸水冷銅壁,生長(zhǎng)速率較快。隨著后續(xù)凝固坯殼生長(zhǎng),鋼液凝固速率逐漸降低,凝固組織生長(zhǎng)速率減小。由于結(jié)晶器內(nèi)初始凝固與鑄坯內(nèi)部CET關(guān)聯(lián)較小,因此僅對(duì)生長(zhǎng)速率在E~G段的變化進(jìn)行討論。

圖5

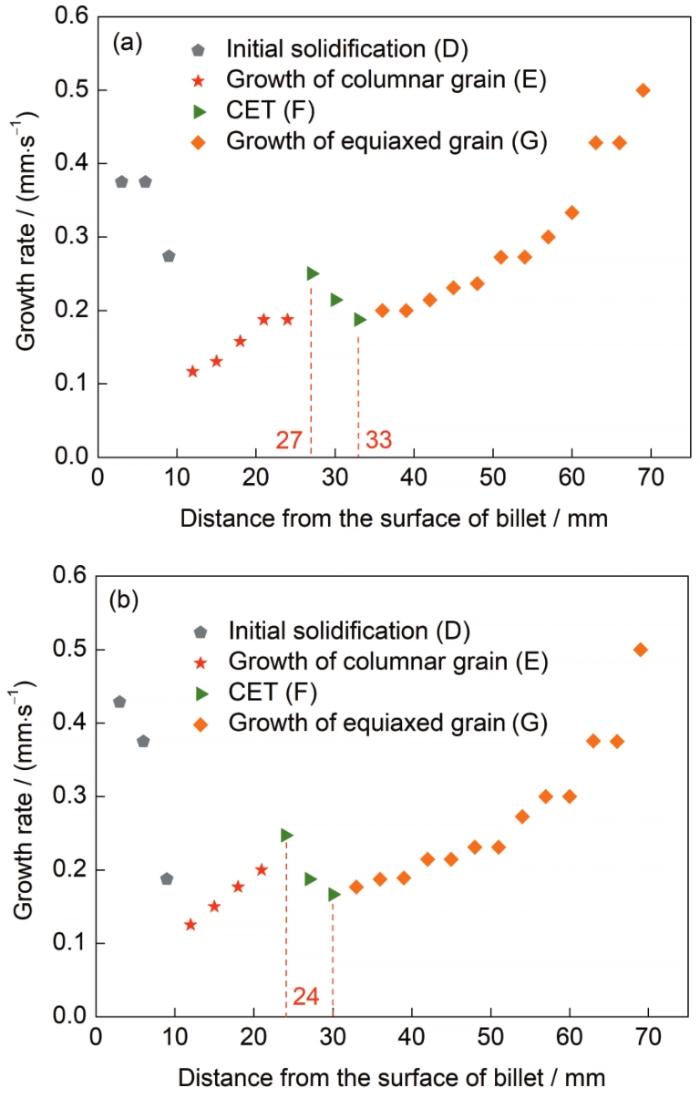
圖5   No.1和No.2鑄坯左側(cè)中心線生長(zhǎng)速率變化

Fig.5   Growth rate changes of solidification structure on the left centerline of billets No.1 (a) and No.2 (b) (CET—columnar to equiaxed transition)

當(dāng)鑄坯離開(kāi)結(jié)晶器進(jìn)入二冷區(qū),隨著外部冷卻水對(duì)鑄坯的冷卻以及鑄坯內(nèi)部總熱量的不斷減少,生長(zhǎng)速率整體上呈現(xiàn)增加的趨勢(shì)。其中E段主要代表鑄坯剛出結(jié)晶器時(shí),鑄坯內(nèi)部柱狀晶穩(wěn)定生長(zhǎng)的階段。此時(shí),熱量沿柱狀晶生長(zhǎng)方向向外近似一維傳遞,伴隨著外部冷卻,凝固組織生長(zhǎng)速率逐漸增大。G段代表鑄坯內(nèi)部等軸晶生長(zhǎng)的階段,此時(shí)鑄坯內(nèi)部熱量相對(duì)更少,由于等軸晶的各向同性,鑄坯內(nèi)部由外向內(nèi)近似等溫凝固,因此該階段凝固組織生長(zhǎng)速率有較大幅度的增加。在柱狀晶向等軸晶轉(zhuǎn)變過(guò)程中,根據(jù)Hunt[8]提出的“機(jī)械阻塞”準(zhǔn)則,當(dāng)?shù)容S晶粒體積分?jǐn)?shù)達(dá)到0.49時(shí),柱狀晶前沿生長(zhǎng)會(huì)被阻斷從而發(fā)生CET,而柱狀晶生長(zhǎng)受阻則會(huì)造成內(nèi)部凝固組織生長(zhǎng)速率的短時(shí)間突降,這與F段相對(duì)應(yīng)。同時(shí),CET的出現(xiàn)使得熱量沿柱狀晶的一維傳輸被阻斷,熱量傳遞效率降低也會(huì)導(dǎo)致生長(zhǎng)速率的減小。因此,F段所處的位置即為鑄坯內(nèi)部CET位置。

在2塊試樣實(shí)際生產(chǎn)過(guò)程中,No.1試樣過(guò)熱度較高,No.2試樣過(guò)熱度較低。根據(jù)已有的研究[7,23,24],較低的過(guò)熱度有利于提高等軸晶形核數(shù),促進(jìn)CET轉(zhuǎn)變并擴(kuò)大等軸晶區(qū),因此,No.2試樣橫斷面等軸晶率更高。溫度梯度和生長(zhǎng)速率的分析結(jié)果顯示,No.2試樣溫度梯度拐點(diǎn)與生長(zhǎng)速率突降位置均更靠近鑄坯表面,即其CET位置更接近鑄坯表面,等軸晶區(qū)更大,這與現(xiàn)有研究[7,23,24]結(jié)果相符。結(jié)合以上對(duì)溫度梯度和生長(zhǎng)速率在由鑄坯表面至中心一維方向上的分析可知,鑄坯內(nèi)部溫度梯度和生長(zhǎng)速率隨著不同凝固階段以及不同凝固組織特征而變化,且在CET位置處皆存在拐點(diǎn)或突變。溫度梯度和生長(zhǎng)速率均可對(duì)連鑄過(guò)程中SDAS產(chǎn)生影響,則在由鑄坯表面至中心方向上也會(huì)存在SDAS的拐點(diǎn)或突變,因此,可以根據(jù)連鑄坯表面SDAS變化特征來(lái)對(duì)鑄坯內(nèi)部CET位置進(jìn)行確定。

3 鑄坯CET位置確定新方法

3.1 CET位置確定原則

如前所述,鑄坯內(nèi)部柱狀晶到等軸晶凝固組織的變化會(huì)影響由鑄坯表面至中心溫度梯度和生長(zhǎng)速率的變化。在CET位置處,凝固組織生長(zhǎng)速率出現(xiàn)一定程度的降低,伴隨著溫度梯度的持續(xù)減小,結(jié)合 式(4)可知,CET位置處SDAS會(huì)出現(xiàn)一定程度突增,這與實(shí)際測(cè)量結(jié)果(圖3)相符,也與前人研究[21,22]中對(duì)于凝固組織和枝晶間距的測(cè)量結(jié)果相吻合。同時(shí),Li等[25]針對(duì)高錳鋼連鑄坯表面至中心鋼液的局部凝固時(shí)間進(jìn)行了數(shù)值計(jì)算,其結(jié)果顯示鑄坯內(nèi)部柱狀晶與等軸晶之間存在局部凝固時(shí)間的較大差異,這一現(xiàn)象將導(dǎo)致該位置處SDAS的突增,這也與本工作的SDAS測(cè)量結(jié)果相符。圖6為實(shí)際鑄坯由表面至中心的部分凝固組織,左側(cè)為柱狀晶區(qū),其二次枝晶比較細(xì)密,右側(cè)為等軸晶區(qū),其二次枝晶較為粗大。在2者交接區(qū)域,存在SDAS的突增現(xiàn)象并伴隨著SDAS的最大增加率,此時(shí),凝固組織二次枝晶發(fā)生了由細(xì)密到粗大的轉(zhuǎn)變,即CET轉(zhuǎn)變。

圖6

圖6   鑄坯內(nèi)部由表面至中心凝固組織典型形貌特征變化

Fig.6   Typical morphological changes of the solidified structure from the surface to the center of the billet

Hunt[8]提出的CET判定模型為：

式中,N0為非均質(zhì)形核密度,m–3；ΔTN為形核所需過(guò)冷度,℃；ΔTC為枝晶尖端過(guò)冷度,可表示為：

式中,V為枝晶尖端移動(dòng)速率,mm/min；C0為合金溶質(zhì)質(zhì)量分?jǐn)?shù),%；D為溶質(zhì)元素在液相中的擴(kuò)散系數(shù)；m為液相線斜率；k為溶質(zhì)分布系數(shù)；Γ為Gibbs-Thomson參數(shù)。此處,根據(jù)前人研究結(jié)果[26]假設(shè)ΔTN在CET情況下相比于ΔTC可忽略不計(jì),則有：

且 式(5)所示Hunt模型可簡(jiǎn)化為：

觀察 式(9)所示CET判據(jù)可知,由鑄坯表面至中心,當(dāng)G小于 式(9)右邊所計(jì)算某一值時(shí),可認(rèn)為鑄坯內(nèi)部發(fā)生CET。對(duì)于同一鋼種,C0及A可近似認(rèn)為是常數(shù),則CET的判斷僅與V和N0有關(guān)。其中,V可近似認(rèn)為是圖5所計(jì)算的變化過(guò)程,即由柱狀晶至等軸晶整體呈現(xiàn)增加的趨勢(shì),在其過(guò)程中間存在短時(shí)間的降低。同時(shí),根據(jù)Hunt[8]提出的“機(jī)械阻塞”準(zhǔn)則可知,柱狀晶前沿等軸晶粒體積分?jǐn)?shù)達(dá)到一定程度后便阻斷柱狀晶的生長(zhǎng),這一準(zhǔn)則在一定程度上意味著CET發(fā)生時(shí)柱狀晶前沿非均質(zhì)形核密度可能發(fā)生突增。因此,Hunt[8]模型本質(zhì)上也是對(duì)生長(zhǎng)速率變化以及非均質(zhì)形核密度由柱狀晶區(qū)向等軸晶區(qū)突增的描述。由于形核密度與枝晶間距的變化具有相似凝固條件[27],故從凝固理論角度來(lái)看這與本研究中枝晶間距的突增現(xiàn)象是基本一致的。然而,實(shí)際碳鋼連鑄坯內(nèi)部非均質(zhì)形核密度的確定較為困難,相比之下,SDAS的測(cè)量則較為簡(jiǎn)便直觀且方法較為成熟。

基于以上分析,本工作基于鑄坯內(nèi)部SDAS突增現(xiàn)象,采用SDAS最大增加率原則對(duì)連鑄坯內(nèi)部CET起始位置進(jìn)行確定,主要過(guò)程如圖7所示。對(duì)于鑄坯橫斷面上任一位置,由鑄坯表面至中心依次挑選典型枝晶,并采用截線法計(jì)算SDAS。隨后,根據(jù) 式(10)計(jì)算由表面至中心相鄰SDAS之間的增加率,當(dāng)SDAS最大增加率出現(xiàn)時(shí),認(rèn)定前一個(gè)枝晶末端為CET起始點(diǎn)。

圖7

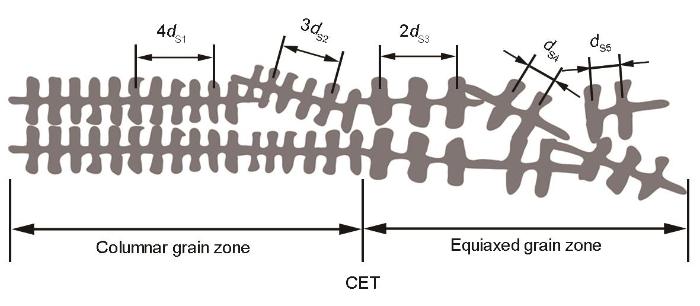
圖7   基于SDAS變化的鑄坯CET判斷過(guò)程示意圖

Fig.7   Schematic of billet CET determination based on the SDAS change (dSi —SDAS of typical dendrite)

式中,RSDAS代表SDAS增加率；dSi 代表典型枝晶SDAS,μm；d(Si + 1)代表相鄰且更靠近中心的典型枝晶SDAS,μm。

3.2 CET位置準(zhǔn)確性

根據(jù)上述CET確定新方法對(duì)2塊鑄坯CET位置進(jìn)行確定,結(jié)果如表4所示。由表可知,No.2鑄坯各位置所確定CET位置較No.1鑄坯均更接近鑄坯表面,即No.2鑄坯等軸晶區(qū)更大,這與二維溫度場(chǎng)分析結(jié)果相符。同時(shí),按照表4所示結(jié)果在實(shí)際鑄坯凝固組織中對(duì)CET計(jì)算位置進(jìn)行標(biāo)注,結(jié)果如圖8所示。由圖可知,所計(jì)算CET起始位置與實(shí)際鑄坯凝固組織特征相吻合,即CET計(jì)算位置外側(cè)為柱狀晶組織,內(nèi)側(cè)為混晶組織。

表4   No.1和No.2鑄坯橫斷面CET位置測(cè)量結(jié)果

Table 4  Measurement results of the CET position on the cross section of billets No.1 and No.2

新窗口打開(kāi)| 下載CSV

圖8

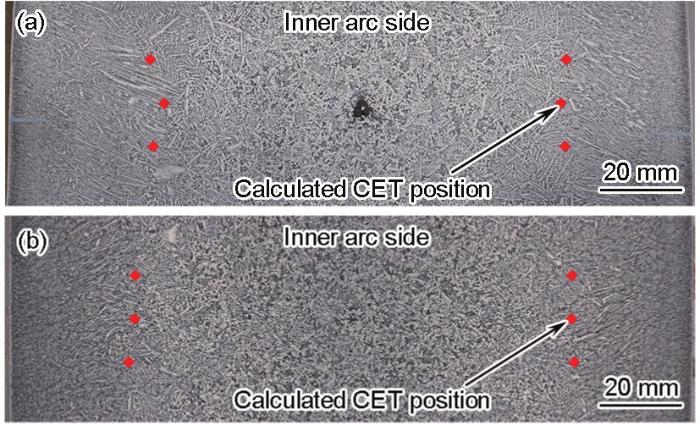
圖8   No.1和No.2鑄坯CET計(jì)算位置

Fig.8   Calculated CET positions of actual billets No.1 (a) and No.2 (b)

為了更為定量地對(duì)計(jì)算所得CET位置進(jìn)行驗(yàn)證,將2塊鑄坯各CET計(jì)算位置平均值與溫度梯度拐點(diǎn)位置進(jìn)行對(duì)比,可知No.1和No.2鑄坯CET位置測(cè)量平均值與溫度梯度拐點(diǎn)值對(duì)應(yīng)程度分別為93.5%和91.7% (最大相對(duì)誤差為8.3%)。隨后,將CET計(jì)算位置與生長(zhǎng)速率突降區(qū)間進(jìn)行對(duì)比,可知2塊鑄坯橫斷面各位置處計(jì)算所得CET位置均處于生長(zhǎng)速率突降區(qū)間內(nèi)。由此對(duì)比結(jié)果可知,SDAS出現(xiàn)最大增加率位置與溫度梯度拐點(diǎn)位置、凝固組織生長(zhǎng)速率波動(dòng)區(qū)間位置基本吻合,結(jié)合前文分析,可以將其作為連鑄坯CET位置判斷的依據(jù)。

綜上所述,本工作對(duì)SCM440冷鐓鋼連鑄坯橫斷面不同位置處SDAS進(jìn)行測(cè)量分析,基于典型枝晶SDAS最大增加速率建立了連鑄坯CET位置定量判斷的新方法：將鑄坯內(nèi)部典型枝晶SDAS最大增加率的起始點(diǎn)作為CET的起始位置。將新方法測(cè)量結(jié)果與鑄坯內(nèi)部凝固組織以及傳熱參數(shù)的數(shù)值計(jì)算結(jié)果進(jìn)行對(duì)比,證明了該方法的有效性。基于連鑄坯實(shí)際凝固組織的CET定量判斷新方法可以為實(shí)際生產(chǎn)中連鑄坯低倍質(zhì)量評(píng)價(jià)以及工藝參數(shù)改進(jìn)提供指導(dǎo)。

4 結(jié)論

(1) 冷鐓鋼鑄坯內(nèi)部CET位置處存在典型枝晶SDAS的突增現(xiàn)象,并基于此提出了將典型枝晶SDAS最大增加率起始位置作為鑄坯CET起始位置的新方法。

(2) 采用新方法對(duì)所選鑄坯CET位置進(jìn)行計(jì)算并據(jù)此判斷2塊鑄坯等軸晶區(qū)分布情況,可知2塊鑄坯等軸晶區(qū)分布情況與實(shí)際凝固組織觀察結(jié)果相符,且計(jì)算所得鑄坯CET位置與鑄坯橫斷面實(shí)際凝固組織特征轉(zhuǎn)變位置相吻合。同時(shí),將計(jì)算所得CET位置與溫度場(chǎng)數(shù)值計(jì)算結(jié)果進(jìn)行對(duì)比,可知計(jì)算所得2塊鑄坯CET平均位置與溫度梯度變化拐點(diǎn)的最大相對(duì)誤差為8.3%,各CET計(jì)算位置均落在生長(zhǎng)速率突降區(qū)間內(nèi),即本工作所提出的CET定量判定新方法是有效的。此方法使鑄坯CET位置判定結(jié)果更為準(zhǔn)確,有利于鑄坯質(zhì)量的精細(xì)化控制。