徐宏揚, 柯海波, 黃火根, 張培, 張鵬國, 劉天偉

中國工程物理研究院材料研究所 江油 621907

摘要

關鍵詞： 非晶合金 ; 鈾合金 ; 納米壓痕 ; 蠕變行為 ; 應力指數

蠕變主要表現為在特定溫度和載荷條件下,材料隨著時間的增長發生的緩慢變形,這種變形即使在應力小于屈服極限時仍具有不可逆性[1]。蠕變性能對于材料的應用至關重要,是影響材料失效的主要因素[1~4],因而掌握材料的蠕變性能參數非常必要。獲取這類參數的常規方法是單軸拉伸蠕變測試法[5],但它需要大量的試樣和較長的測試時間。與此不同,采用納米壓痕測試技術也能獲得材料的蠕變性能指標[6,7],它既省時省料,對試樣形態的要求也不高,且特別適用于薄膜、薄帶等體積很小的材料以及難于加工的高硬、脆性材料[8,9]。

非晶合金是一類先進的金屬材料[10],在航空航天、軍事、體育等領域具有廣闊的應用,因而其蠕變性能得到廣泛關注。由于U金屬的高密度和可裂變性,作為一個特殊的分支,鈾基非晶合金在核工業領域具有重要的應用前景。尤其是,近期研究[11,12]表明,這類非晶合金的抗腐蝕性能和力學性能顯著優于晶態鈾合金,有望成為核相關領域的結構材料。但目前為止,這類材料的蠕變行為仍缺乏研究。

盡管鈾基非晶合金自20世紀50年代開始已有報道[13],但由于早期形成的合金體系[14]非晶形成能力較弱,且熱穩定性較差,難以開展系統的蠕變性能研究。近期,本課題組通過研究發現并制備出不同體系的穩定鈾基非晶合金體系[11,12,15]。在本工作中,針對可形成單一非晶相的新型U-Fe-Al非晶合金,利用熔體甩帶方法制備出高質量的非晶條帶樣品,采用納米壓痕測試技術研究了其蠕變性能,主要考察不同加載速率與載荷條件對蠕變行為的影響。

1 實驗方法

實驗選取的非晶合金成分為U65Fe30Al5 (原子分數,%)。實驗原料為純度均高于99.9%的金屬U、Fe和Al。按照相應成分配料后, 采用NMS-II型小型亞穩合金制備爐, 在高純Ar氣(純度>99.999%)保護下制備質量約5 g的母合金錠。為保證成分均勻, 反復熔煉母合金4次以上,破碎后用于Cu輥急冷甩帶, Cu輥線速率約50 m/s, 頂吹氣體壓差約為0.04 MPa。最后獲得尺寸為寬約2 mm、厚約30 μm的非晶條帶樣品,其形態和韌性參見文獻[11]。為驗證條帶的非晶本質,利用EMPYREAN型X射線衍射儀(XRD,CuKα)進行測試。

本工作采用Hysitron TI 950納米壓痕系統微尺度蠕變測試,該儀器具有極高數據采集速率(最高至30000 s-1)、優異的位移和載荷分辨率(分別為1 nm和1 μN)[16]。測試時選擇樣品的自由面,即合金甩帶時未直接與Cu輥接觸的表面,因為在冷卻過程中該面不會受Cu輥表面形態的影響,具有高的表面平整度和均勻度。測試前,首先保持樣品自由面在上使其粘于平整潔凈的金屬樣品臺面,再使用丙酮對樣品表面進行清潔處理,最后置于納米壓痕儀的樣品臺上。

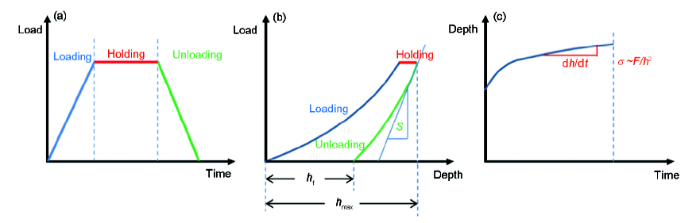
本工作的納米壓痕蠕變測試采用如圖1a所示的加載函數,包括加載-保載-卸載3個階段,單次蠕變測試獲取的理想載荷-深度曲線如圖1b所示,而理想的標準蠕變曲線(深度-時間曲線)如圖1c所示。 測試方法包括等加載速率和等加載載荷2種,具體為：在20 mN/s加載速率下,選擇載荷10、20、50、100和200 mN;在100 mN載荷下,選擇加載速率2、5、10、20、50和100 mN/s 。對于單個加載載荷與加載速率,采取5次以上實驗然后進行平均處理,以保證實驗的重復性與可靠性。

圖1   納米壓痕測試過程的加載函數與理想特征曲線

Fig.1   Loading function and ideal characteristic curves for nanoindentation creep (S—contact stiffness, h—indentation depth, F—load, hmax—maximum indentation depth, hf—permanent deformation depth after fully unloading, t—time, σ—stress)(a) load-time curve (b) load-depth curve (c) standard creep depth-time curve

2 實驗結果

圖2為U65Fe30Al5合金的XRD譜。可以看到,在30°~ 40°之間呈現出典型的饅頭狀非晶態漫散衍射峰特征, 確認該合金為單相的非晶結構。

圖2   U65Fe30Al5非晶合金的XRD譜

Fig.2   XRD spectrum of U65Fe30Al5 amorphous alloy

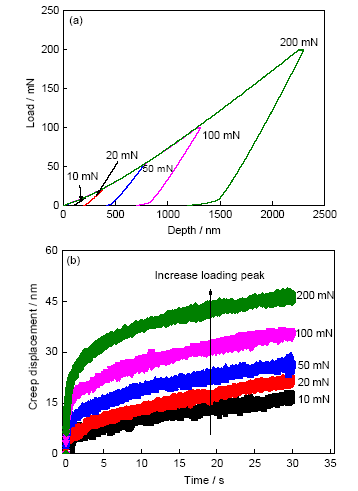
圖3為U65Fe30Al5非晶合金以20 mN/s的速率加載至不同峰值載荷下的蠕變曲線。由圖3a可見,樣品的最大壓入深度隨著峰值載荷的增加不斷增大,由10 mN下210 nm增至200 mN下的2300 nm,同時不同峰值載荷下加載階段的載荷-深度曲線完全重合,表明該樣品的成分與結構具有較好的均勻性,也表明實驗數據具有很好的重復性和可靠性。圖3b為載荷保持階段即蠕變階段樣品蠕變位移隨時間的變化曲線,為便于比較,起始蠕變位移和時間均進行了歸零化處理(下同)。隨著峰值載荷的增大,蠕變位移也不斷變大,由10 mN下的15 nm增加至200 mN下的45 nm,且樣品進入穩態蠕變的時間不斷延長,由10 mN下的5 s變至200 mN下的10 s左右,這說明在較高的峰值載荷下,較大的壓入深度引起更大的變形區域,為進入穩態蠕變需要在更大尺度上進行原子重排,因此所需的時間也更長。

圖3   U65Fe30Al5非晶合金在不同載荷條件下蠕變30 s的載荷-深度曲線和蠕變位移-時間曲線(起始蠕變位移和時間進行歸零化處理)

Fig.3   Load-depth (a) and creep displacement-time (b) curves during 30 s nanoindentation creeping under different peak loads (The curves in the Fig.3b are offset from the origin points of the creep process)

圖4為U65Fe30Al5非晶合金在恒定峰值載荷(F=100 mN)不同加載速率條件下的蠕變曲線。其中圖4a為載荷-深度曲線,為了能夠清晰比較加載速率的效應,對不同加載速率的曲線進行了等間距平移處理。從中可見,在100 mN的載荷條件下,壓頭最大的壓入深度約為1300 nm,隨著加載速率的增加,保載階段的蠕變位移也在增大,其中加載和卸載階段的曲線保持平行,卸載段曲線可用于計算材料的模量,這說明該材料不同位置的模量保持不變,具有相對均勻的結構。圖4b給出了蠕變位移隨時間的變化曲線。可看出蠕變位移隨著加載速率的增加而增大,由2 mN/s下的15 nm增大至100 mN/s下的40 nm。另外,在相同的載荷條件下,加載速率對材料進入穩態蠕變的起始時間影響并不大,基本都在5 s左右。

圖4   U65Fe30Al5非晶合金在不同加載速率下蠕變30 s的載荷-深度曲線(平移處理后)和蠕變位移-時間曲線

Fig.4   Load-depth (a) and creep displacement-time (b) curves during 30 s nanoindentation creeping under different loading rates (Curves in Fig.4a are translation-transformed)

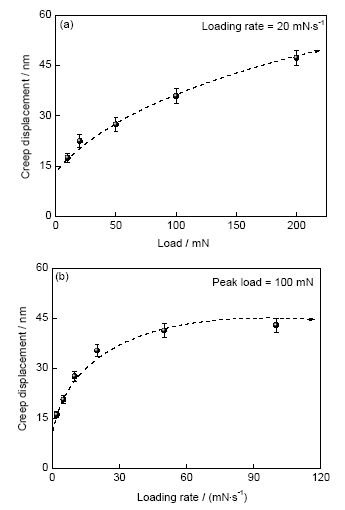
為了能夠更加直觀地比較加載速率與峰值載荷對蠕變行為的影響,根據圖3和4可以獲得U65Fe30Al5非晶合金蠕變30 s后蠕變位移值,該值隨加載載荷與加載速率的變化趨勢由圖5給出。可以看出,在30 s的蠕變時間內,峰值載荷與加載速率的增大均會引起最終蠕變位移的增加,但兩者之間仍有一些差別。一方面,當僅改變峰值載荷時,蠕變位移會隨著峰值載荷增大一直增加(圖5a),即使在200 mN的條件下仍未達到飽和。Ma等[17]研究了峰值載荷對CuZrAl和CuZrAlTi非晶薄膜的蠕變位移影響,其結果顯示,隨著峰值載荷從1 mN增大至16 mN,蠕變位移也會持續增大。Huang等[18]研究了峰值載荷對鈦基非晶合金的蠕變行為影響,同樣發現這種變化趨勢。可見,這些工作與本實驗的結果一致。這意味著峰值載荷對蠕變位移具有積極作用,隨著峰值載荷的增加,材料在壓頭下的變形區域會一直增大,因為需要更大尺度內的原子局域重排以適應壓頭,由此引起蠕變位移的持續增加,這種變化趨勢隨著峰值載荷的加大很可能還會繼續下去。另一方面,當僅改變加載速率時,蠕變位移則隨著加載速率的增加先增大后基本恒定(圖5b),其中當加載速率小于50 mN/s時,蠕變位移存在這種增長趨勢,而當大于50 mN/s時,蠕變位移基本趨于飽和值45 nm,繼續增大加載速率對最終蠕變位移的影響不大。Pang等[19]研究了加載速率對Cu49.3Zr50.7非晶合金蠕變位移的影響,發現在加載速率小于1 mN/s的條件下,蠕變位移一直呈增大趨勢,但未報道更大加載速率下的實驗結果。可見,在低加載速率情況下,本實驗結果與文獻[19]現象相符。

圖5   U65Fe30Al5非晶合金的蠕變位移隨載荷與加載速率的變化趨勢

Fig.5   Variation of creep displacement versus peak load (a) and loading rate (b) during the nanoindentation creeping of U65Fe30Al5 amorphous alloy

3 討論

在納米壓痕測試中,對于自相似的Beckvich壓頭測試,其應變率與應力滿足以下標度關系[20,21]：

$\begin{array}{c}\dot{?}=\frac{1}{?}\frac{\mathit{dh}}{\mathit{dt}}\end{array}$(1)

$\begin{array}{c}\mathit{\sigma ~}\frac{?}{{?}^2}\end{array}$(2)

式中, $\begin{array}{c}\dot{?}\end{array}$為應變率,h為瞬時深度(即壓頭位移), $\begin{array}{c}?\end{array}$為應力,F為載荷,t為時間。在加載載荷條件下,h隨t的變化可由以下經驗方程進行描述[20]：

$\begin{array}{c}?={?}_0+?(?-{?}_0{)}^{?}+\mathit{kt}\end{array}$(3)

式中,h0和t0為蠕變起始點的壓頭深度與時間,a、b和k均為擬合參數。

對于穩態蠕變材料,應力與應變率之間滿足以下關系[20]：

$\begin{array}{c}\dot{?}=?{?}^{?}\end{array}$(4)

式中,n為應力指數, C為常數。通過等溫條件下 $\begin{array}{c}\mathit{lg}\dot{?}\end{array}$- $\begin{array}{c}\mathit{lg\sigma }\end{array}$曲線圖的斜率可計算獲得n。n表示材料穩態蠕變過程中應變率對應力的敏感度,可反映材料內部結構的信息。為了獲得U65Fe30Al5非晶合金的n,用式(4)進行數據擬合。

圖 6a為U65Fe30Al5非晶合金以20 mN/s加載至100 mN蠕變30 s的h-t擬合曲線。可見,擬合曲線與實驗結果相吻合,擬合的相關系數R2 (=0.985)也接近1。圖6b為在上述條件下的應力指數分析圖。可以看出,在蠕變初始階段,應力指數n高達282,說明此階段的材料變形對應力極敏感,而當蠕變趨于穩態之后,應力指數n降至89,這一穩態值對應著此加載條件下材料的應力指數。

圖6   U65Fe30Al5非晶合金蠕變過程中的實驗與擬合曲線(式(3))和應力指數變化圖

Fig.6   Experimental and fitting curve (Eq.(3)) (a) and the variation of stress exponent derived from stress-strain rate relationship curve (b) during the nanoindentation creeping of U65Fe30Al5 amorphous alloy (h0—initial creep displacement, t0—initial creep time, a and k—fitting parameters)

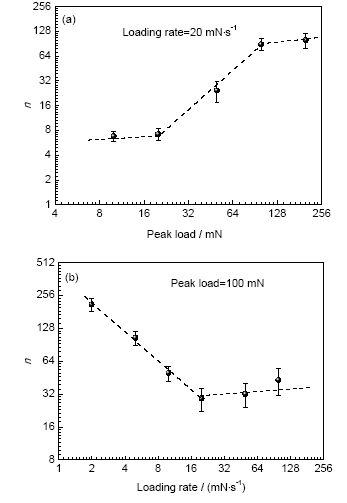
通過以上處理方法對其它所有蠕變曲線進行擬合(擬合后相關指數R2均大于0.96),獲取U65Fe30Al5非晶合金在不同條件下的n值,它對載荷與加載速率的依賴關系由圖7給出。由圖7a可見,隨著載荷的增大,n逐漸增大,其變化趨勢可分為3段：當載荷低于20 mN時,n約為7;當高于100 mN時,n約為90;當大于20 mN而低于100 mN時,n由7快速增長至90。由圖7b可知,隨著加載速率的增大,n快速降低,當加載速率大于20 mN/s時,n基本不變,保持在40左右。對于非晶合金而言,Huang等[18]通過Ti基塊體和條帶樣品的蠕變行為研究發現,相對于條帶樣品,塊體樣品具有更高的應力指數值,且隨著接觸深度即載荷的增大,應力指數會持續增大。這一結果與圖7a中的現象一致。

圖7   U65Fe30Al5非晶合金穩態蠕變過程中的應力指數-載荷曲線與應力指數-加載速率曲線

Fig.7   Curves of stress exponent-peak load (a) and stress exponent-loading rate (b) during the steady creeping of U65Fe30Al5 amorphous alloy(n—stress exponent)

目前,已經有很多研究報道了納米壓痕蠕變中加載速率與峰值載荷對應力指數的影響,包括一些晶態材料以及氧化物玻璃。例如對于純的多晶Al和單晶Ni3Al,隨著峰值載荷的增大,其蠕變過程會從原子擴散向位錯攀爬并最終向滑動控制的蠕變逐漸演變,從而引起應力指數的顯著改變[20]。但對于非晶合金,由于缺乏晶態合金中的位錯等結構缺陷,變形行為一般根據“自由體積”[22]或者“剪切變形區”[23]模型進行解釋,通常認為,隨著峰值載荷的增加,其結構中的“自由體積”或“剪切變形區”體積會不斷變化,進而引起應力指數的變化[19,20,24]。在納米壓痕測試中,由于壓頭形狀的限制,材料中塑性變形一般局限在較小的體積中,并且具有非均勻應力場和強梯度應變場的特征,這會顯著影響非晶合金中剪切變形區的演化,最終表現出壓頭周圍剪切帶形態的改變,從而引起應力指數的變化。這種行為已在鋯基非晶合金[25]中得到證實,研究發現隨著載荷的增大,壓頭周圍變形區中剪切帶圖案會由較小區域向半圓形區域并最終向多剪切帶交叉演化,并引起應力指數的改變。由此可見,對于非晶合金材料,應力指數與應力狀態、剪切體積之間存在著密切的關系。

在增大載荷的條件下,非晶的變形更趨向非局域性,需要更大尺度與范圍內的原子或剪切變形區進行重排適應,因而具有更大的應力指數,這與圖7a結果一致。對于同一峰值載荷條件,不同的加載速率也會引起應力指數的變化,不過當快速加載時,特定應力條件下的最大剪切變形區域可能存在一個閾值,從而導致應力指數基本恒定,這也許是圖7b現象的物理機制。

與常規晶態材料相比,非晶合金一般具有較高的應力指數[18,24,26]。幾種不同材料的應力指數由表1給出。在近似相同的測試條件下,非晶合金和氧化物玻璃等無序體系的應力指數顯著高于多晶氧化物B6O。例如對于鈦基非晶,它經歷了更大時間尺度的蠕變,但其應力指數(n=5)比B6O (n=0.14)的數值大了1個數量級。這意味著無序體系材料在應力作用下更容易發生變形,具有更強的應力敏感性,這可能與無序材料中具有更多的自由體積,原子堆積密度小于晶態材料有關。實際上,非晶合金的密度均低于同成分的晶態合金,存在著更多的自由體積區域,這些區域在外力作用下更易于變形,因而使得非晶合金材料具有更高的應力敏感性,即更大的應力指數。

4 結論

(1) U65Fe30Al5非晶合金的室溫蠕變位移與峰值載荷、加載速率呈正相關性。

(2) 該非晶的應力指數與峰值載荷之間存在正相關性,隨著載荷增加而增大,這主要跟參與剪切變形的體積增大有關。

(3) 該非晶的應力指數隨加載速率的變化存在一個閾值,當低于該值時二者呈現負相關性,當高于該值時應力指數基本不變

來源--金屬學報