分享:Al薄膜對玻璃纖維增強樹脂基復合材料電磁性能的影響
陳育秋
摘要
利用高頻電磁場計算軟件FEKO對Al薄膜與玻璃纖維增強樹脂基復合材料的電磁波反射率進行了仿真計算。研究了復合材料介電常數實部εr、電損耗角正切tanδε、磁導率μr及磁損耗角正切tanδμ對反射率的影響,并通過仿真計算與實際測試結果對比,確定了仿真模型中玻璃纖維增強樹脂基復合材料的等效電磁參數。研究了Al薄膜與玻璃纖維增強樹脂基復合材料結構中Al薄膜厚度對反射率的影響,仿真計算與測試結果表明,Al薄膜厚度對復合材料的反射率影響較大,Al薄膜與玻璃纖維增強樹脂基復合材料結構中存在一個最佳電阻值,使該結構諧振反射最小。根據傳輸線理論,利用MATLAB對諧振最強時對應電阻的大小進行了求解。通過計算不同結構的Al薄膜與玻璃纖維增強樹脂基復合材料,得到了仿真模型中Al薄膜與磁控濺射制備Al薄膜的厚度關系。確定了仿真模型中各材料的等效電磁參數,仿真計算結果與測試結果吻合較好。
關鍵詞:
電磁波入射到塊體金屬時,由于塊體金屬與空氣的波阻抗存在較大差別,電磁波在金屬表面會發生全反射。從導體的“趨膚深度”定義可知,電磁波的電磁分量將隨著入射深度的增加呈指數衰減,通常將電場分量衰減到原來的1/e時的厚度定義為“趨膚深度”。對于塊體Al,電磁波在頻率為10 GHz時,其“趨膚深度”為815 nm。當金屬膜的厚度小于趨膚深度時,會表現出很多有別于塊體材料的電磁性能,如電阻性能等。金屬電阻形成源于自由電子發生碰撞,碰撞后電子失去了從外電場獲得的定向速度。這種碰撞可能發生于電子-晶格、電子-雜質、電子-晶界和電子-表面。在塊體材料中,電子-表面碰撞的次數與總碰撞次數之比極小,可以忽略,因而塊體材料的電阻率與其尺寸幾乎無關。但對薄膜而言,當其表面特征尺寸與該溫度下電子自由程相當時,電子-薄膜的表面碰撞呈非鏡面反射(反射方向與入射方向無關,亦即漫反射),電阻率就會隨表面狀態改變。超薄金屬膜在與電磁波交互作用下,高的表面原子比例導致界面極化,造成表面多重散射,因此超薄金屬膜具有高的表面阻抗。近年來,隨著高阻抗表面設計電磁功能材料的出現,超薄金屬膜與介質復合材料設計成為熱點[1~5]。傳統的電磁功能材料大多依賴于金屬結構的電磁諧振,其表面阻抗只能在諧振頻率附近極窄的頻帶內與自由空間阻抗匹配,因而帶寬極窄。為了實現寬頻帶的電磁性能,可以用電阻膜(超薄金屬膜)結構替代金屬結構,將電磁諧振轉化為電阻膜結構與基板和金屬背板之間的電路諧振。因為電路諧振相對于頻率的變化比較穩定,其表面阻抗能在諧振頻率附近很寬的頻帶內與自由空間阻抗匹配,從而實現在電磁波寬頻帶內的極低反射。金屬膜與介質復合材料結構在天線及吸波體設計中有重要的應用[6~9],并且金屬膜對復合結構電磁性能的影響對最后材料的設計起到至關重要的作用,本工作以Al薄膜為例研究非磁性金屬薄膜在此結構中對電磁性能的影響。目前,制備高阻抗電磁功能材料中的金屬阻抗膜的主要方法為絲網印刷及噴涂法[10,11],本工作采用磁控濺射方法制備高阻抗Al薄膜,薄膜厚度通過調控磁控濺射的時間來控制。
隨著計算機硬件和數值計算技術的迅速發展,數值模擬成為與實驗技術和理論研究并行發展的第三種科學研究方法。材料的電磁波傳輸性能模擬與計算是利用電磁場計算軟件來分析電磁波與材料作用后的反射與透射等問題。設計高阻抗表面電磁功能材料具有廣闊的應用前景[4,11],是功能材料和復合材料研究領域的一個重要的研究方向。盡管大量的可設計參量為設計者提供了充分的設計空間,不過,要設計出性能良好的電磁功能材料也需要付出巨大的人力、物力,耗費較長的時間周期。采用計算機軟件進行仿真計算協助設計可以節約成本、提高效率和縮短設計周期。電磁場問題均遵守電磁理論基礎——Maxwell方程組,所有的電磁仿真軟件的最終目的即為求解Maxwell方程組。求解Maxwell方程組的方法主要為矩量法(MOM)、有限元方法(FEM)及有限差分法(EDM)。本工作利用FEKO軟件的矩量法對Al薄膜與玻璃纖維增強樹脂基復合材料結構進行仿真計算,利用MATLAB軟件對諧振電阻值進行求解。
采用LLFJ-600型內置平面靶磁控濺射儀,選用純Al (純度為99.9%)作為靶材,制備不同厚度的Al薄膜。基片選用厚度為25 μm的聚酯膜(相對介電常數為1.8),鍍膜前基片用丙酮擦拭并經氮離子轟擊,安裝在靶下面可旋轉的滾筒上,保證基片不加熱。基片至靶間的距離為120 mm,真空室預真空3×10-3 Pa,通入Ar氣,工作壓強0.5 Pa,濺射功率300 V×2.8 A,沉積速率約1.0 nm/s。在其它工藝參數保持不變的情況下,通過改變鍍膜時間來調整Al薄膜的厚度,采用Alpha-Step IQ接觸式表面形貌分析儀測試薄膜的厚度。實驗中的玻璃纖維布采用EW100無堿玻璃纖維布,樹脂使用聚乙烯基酯樹脂(牌號3201)。每層玻璃纖維布的厚度約為0.1 mm,玻璃纖維體積分數約為45%,每層玻璃纖維布的樹脂含量約為3 g,采用手糊成型方法制備玻璃纖維增強樹脂基復合材料(以下簡稱為復合材料),使用Inspect F50型掃描電子顯微鏡(SEM)觀察復合材料的形貌。
很多情況下,用反射率來表征材料的電磁性能。電磁波反射率測試曲線表示在介質底面有全反射體如金屬板的測試結果。此時,透射率為0,反射率與吸收率的和為1。
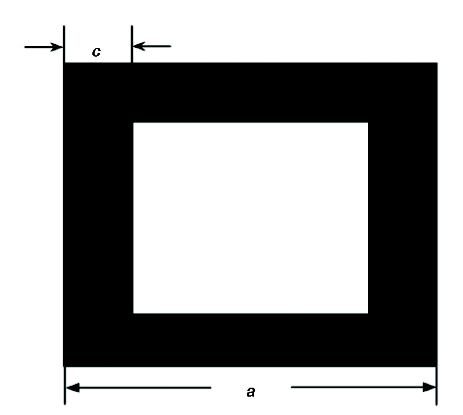
首先,利用良導體襯板Al板來標定零點,測量基片的反射率(基片后面未放置良導體襯板)所得結果與暗室背景的反射率基本一致。可見,電磁波在基片中的傳輸特性與在自由空間的傳輸特性近乎相同。選用不同尺寸的理想導體Al箔單元構成的周期結構(頻率選擇表面)單元形狀如圖1所示,單元尺寸分別為a=48 mm、c=7 mm及a=40 mm、c=5 mm,將其用膠帶牢固的粘貼在3 mm的復合材料表面(200 mm×200 mm),由于頻率選擇表面具有頻率選擇特性,在固定的頻段對電磁波有明顯的透過和反射作用,不同尺寸的單元構成的頻率選擇表面對不同的頻段具有選擇透過和反射的作用,并且Al箔可視為純導體,可以用此模型確定復合材料的等效電磁參數。Al薄膜與復合材料反射率測量時采用相同的方法,本工作設計了2種Al薄膜與復合材料結構,一種是Al薄膜在復合材料表面,另一種是Al薄膜在復合材料的中間位置,這樣設計的目的是因為空氣與介質的波阻抗不同,電磁波在空氣與介質中的波長也不相同,Al薄膜在復合材料中不同位置的阻抗匹配需要不同的電阻值。測量的頻率范圍為4~18 GHz,電磁波的入射角β=6.00°,微波測試儀器采用HP-8350B Sweep Oscillator和HP-8757C Scalar Network Analyzer。
圖1 頻率選擇表面單元
Fig.1 Schematic of frequency selective surface unit
FEKO軟件可以分析薄介質片、多介質體及平面分層媒質等復雜問題[12],本工作應用該軟件進行Al薄膜與玻璃纖維增強樹脂基復合材料結構的仿真計算。
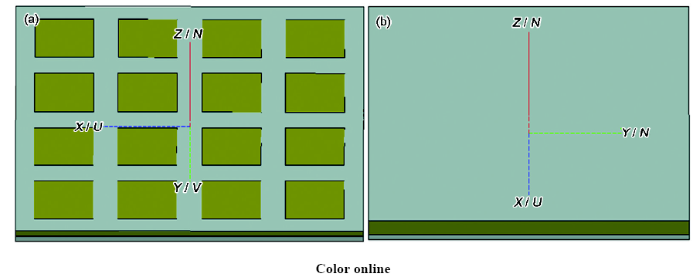
建立模型時,首先根據復合結構的實際結構建立一個多層結構的幾何模型,本工作涉及的2種模型結構如圖2所示,圖2a為Al箔頻率選擇表面、復合材料與金屬底板結構模型,金屬底板為反射層,其中上面的灰白周期單元為鋁箔頻率選擇表面,下面的綠色長方體為復合材料基體,最下面的灰白長方體為金屬底板。圖2b為Al均勻薄膜、復合材料與金屬底板結構模型,模型中最上面的灰白平面為Al均勻薄膜,Al薄膜下面的綠色長方體為復合材料,最下面的灰白長方體為金屬底板。模型建立后,對模型的各部分進行參數設置。選擇外加激勵電磁波的類型,仿真模型中,激勵源選擇垂直均勻平面波;設置電磁波的幅值、相位角及頻率范圍,仿真模型選擇的平面波幅值為1,相位角為0°,頻率范圍為2~18 GHz;接著選擇四面體網格對模型進行劃分,網格的大小選擇為λ/8 (λ為該頻率的電磁波在材料中對應的波長),在分頻段計算中,選擇高頻率所對應的波長的1/8的網格大小進行劃分,保證劃分網格的適應性;選擇合適的計算方法,仿真模型選擇快速多極子方法進行求解計算,在保證精確度的同時提高計算效率;最后對模型進行求解設置,對近場即反射率進行求解。
圖2 2種復合結構仿真模型
Fig.2 Simulation models of two kinds of composite structures (U, V, N represent the three vectors in workplane coordinate system, corresponding to X, Y, Z directions in the global coordinate system, respectively)
本研究Al薄膜與復合材料電磁參數的設定十分重要,包括復合材料的介電常數(εr,tanδε)和磁導率(μr,tanδμ),Al薄膜的電導率σ、磁導率(μr,tanδμ)和厚度,這些電磁參數設定是否合理決定著所建立的模型對電磁波反射率的計算是否準確可靠。一些常用纖維、樹脂及其構成的復合材料體系的介電常數如表1[13]所示。
表1 纖維、樹脂及其構成的復合材料體系的介電性能[
Table 1 Dielectric properties of fiber, resin and its composites at 20 ℃, 10 GHz[
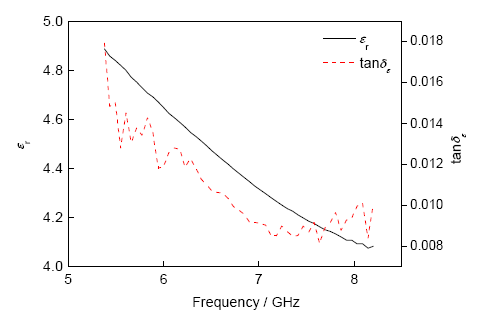
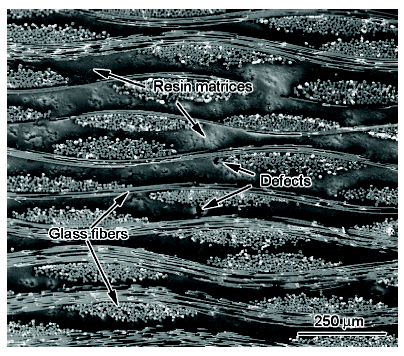
從表1可以看出,由于其制備工藝及含量等因素的影響,纖維、樹脂及其構成的復合材料體系的介電性能在同一頻率的介電性能是變化的,本工作采用的EW100玻璃纖維增強聚乙烯基酯樹脂基復合材料體系的介電性能在不同的頻率也是變化的(圖3)。所以在給計算模型設定材料的介電常數時,所測量的復合材料的介電常數只能作為參考數據,原因有三:一是對于同一種材料,其制備方法、含膠量不同及成型工藝中不可避免存在缺陷,如圖4復合材料截面SEM像所示,材料的介電常數會相應發生變化;二是在測試過程中,由于測試環境、設備等條件的限制,以及測試中不可避免的誤差等因素影響,即使輸入的介電常數是準確的,但模擬結果仍可能與實測結果有偏差;三是層板結構為非理想勻質材料,每一層的介電常數是變化的,在建立模型過程中由等效處理也會帶來誤差。因此需要尋找一個合理的等效介電常數εeff,使仿真結果與實驗結果相符[14,15]。
圖3 復合材料的介電常數實部εr及電損耗角正切tanδε
Fig.3 εr and tanδε of the composite
圖4 復合材料截面SEM像
Fig.4 SEM image of the composite section
本工作通過一系列實驗模擬計算材料的反射率,并與實驗測試結果進行對比,將計算結果與實測結果最接近時所設置的電磁參數作為材料的等效電磁參數。
玻璃鋼本身近似為透波材料,對電磁波的吸收很少,要確定其等效介電常數,先要將其放在一個吸波結構中進行估算,頻率選擇表面具有頻率選擇特性,在固定的頻段對電磁波有明顯的透過和反射作用,由單層頻率選擇表面、復合材料和金屬反射層可以構成一個吸波結構。為保證建立的模型中只有復合材料的電磁參數為未知量,頻率選擇表面采用導體金屬Al箔制備,Al箔可視為理想導體。
選取單元尺寸a=48 mm、c=7 mm的Al箔頻率選擇表面與復合材料組成一個復合結構,建立計算模型,確定復合材料的電磁參數,再用其它不同單元的頻率選擇表面替換,對復合材料的電磁參數進行驗證。
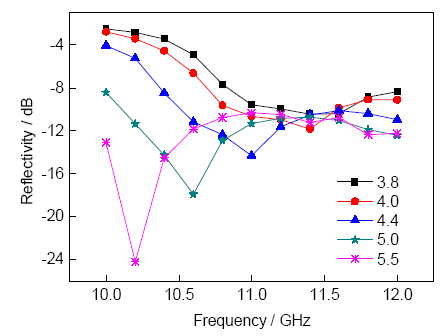
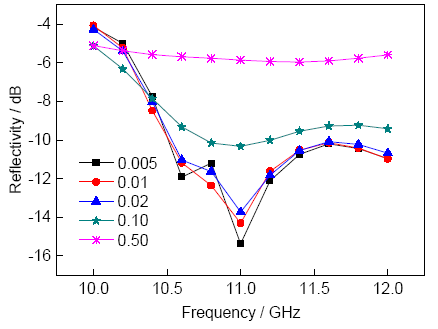
要確定復合材料的電磁參數,首先需分析介電常數實部εr、電損耗角正切tanδε、磁導率實部μr和磁損耗角正切tanδμ對材料的反射率的影響。改變εr,將其它電磁參數設為定值,材料的反射率如圖5所示。εr取3.8、4.0、4.4、5.0及5.5時,對應的反射率最低點分別為11.6、11.4、11、10.6和10.2 GHz,隨著εr的增大,反射率最低點向低頻移動,反射率最小值也隨著發生相應的變化。改變tanδε,將其它電磁參數設為定值,材料的反射率如圖6所示。tanδε取0.005、0.01、0.02、0.10及0.50時,對應的反射率最小值分別為-15.4、-14.3、-13.7、-10.3及-5.9 dB,反射率最低點位置基本保持不變。可見,電損耗角正切的變化沒有引起反射率最低點位置的變化,主要對反射率數值大小有影響。
圖5 εr對復合材料反射率影響
Fig.5 Reflectivity curves of composites with different εr
圖6 tanδε對復合材料反射率的影響
Fig.6 Reflectivity curves of composites with different tanδε
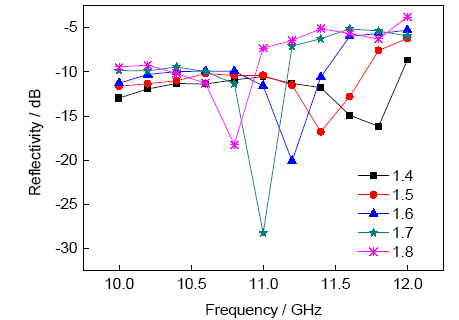
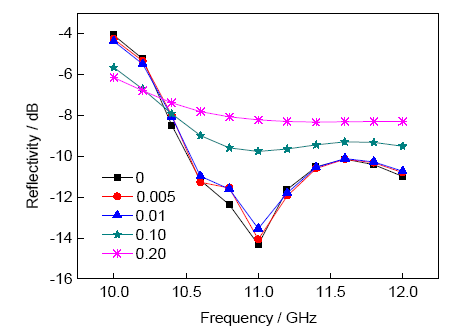
圖7和8分別為復合材料μr和tanδμ取不同值時對應材料的電磁波反射率。可以看出,μr對反射率的影響與εr相似,主要對反射率最低點位置產生影響。μr取1.4、1.5、1.6、1.7及1.8時,對應的反射率最低點分別11.8、11.4、11.2、11.0及10.8 GHz,隨著μr的增加,最低點位置向低頻移動。tanδμ對反射率的影響與tanδε相似,tanδμ取0、0.005、0.01、0.10及0.20時最低點位置基本不變,主要影響反射率大小。
圖7 磁導率實部μr對復合材料反射率的影響
Fig.7 Reflectivity curves of composites with different μr (μr—real part of magnetic permeability)
圖8 磁損耗角正切tanδμ對復合材料反射率的影響
Fig.8 Reflectivity curves of composites with different tanδμ (tanδμ—magnetic loss tangent)
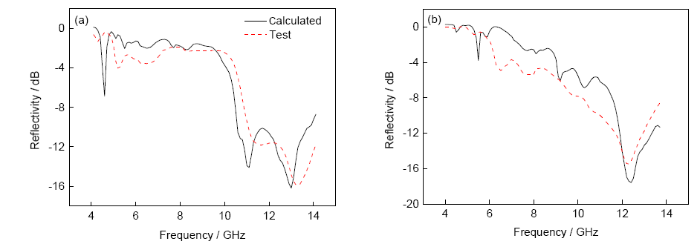
基于εr、tanδε、μr和tanδμ對材料反射率的影響,并考慮復合材料本身為非磁性材料,復合材料的電磁參數在仿真計算中假設為:εr=4.4,tanδε=0.01,μr=1,tanδμ=0。單元尺寸a=48 mm、c=7 mm的Al箔頻率選擇表面與3 mm復合材料組成的復合結構仿真計算的結果與實測數據如圖9a所示。仿真計算與實測曲線的反射率最低點位置約有0.2 GHz偏差,在11 GHz處的反射率大小偏差約為2 dB,在13 GHz處的大小基本相同,總體上2曲線趨勢一致,吻合較好。用單元尺寸a=40 mm、c=5 mm的Al箔頻率選擇表面替換單元尺寸a=48 mm、c=7 mm頻率選擇表面進行仿真驗證,計算結果與實測數據如圖9b所示。仿真計算與實測曲線的反射率最低點位置相同,數值大小有2 dB的偏差,其它頻段有微小偏差,但總體上2曲線的趨勢也是一致的。這里為了簡化只列舉一個驗證模型,其它驗證模型的對比結果與此模型基本相同,計算與測試曲線趨勢基本一致,驗證了所假設的復合材料電磁參數的設置是合理的。存在偏差的主要原因是:由圖3可知,測試得到的參數εr和tanδε隨頻率是變化的,而為了計算方便,本工作采用的是固定的εr和tanδε;其次是制備工藝誤差。
圖9 復合材料反射率計算與測試對比曲線
Fig.9 Reflectivity curves of calculated and test results of composites at the unit size of a=48 mm, c=7 mm (a) and a=40 mm, c=5 mm (b)
對于連續均勻的金屬薄膜材料,在FEKO仿真計算時不需要設定參數εr和tanδε,只需設置μr、tanδμ及塊體材料電導率σ等基本參數。由于Al是非鐵磁性材料,所以μr=1,tanδμ=0,Al塊體材料的電導率σ=3.816×107 S/m。當薄膜厚度在趨膚深度以內時,軟件中給出的金屬表面阻抗Zs的計算公式為:
式中,j為虛部,dm為金屬膜的厚度,δskin為金屬的“趨膚深度”。δskin=
采用磁控濺射工藝制備的Al薄膜與塊體Al的物理特性不同,采用磁控濺射法在均勻連續的聚酯膜上鍍Al薄膜,薄膜的初始生長模式屬于島狀模式,其間經歷島狀膜、網狀膜和連續膜3個階段。本課題組前期工作[16~22]表明:島狀膜階段對應的薄膜厚度極薄,該階段的薄膜的直流電導率極小;隨著薄膜厚度逐漸增加,薄膜生長進入到網狀膜階段,該階段電導率急劇增加;薄膜厚度繼續增加,電導率上升緩慢,并趨于定值形成連續結構。仿真計算中,對薄膜的設置是理想的均勻薄膜,而磁控濺射生長的薄膜在成膜初期是以島狀生長模式進行的,粒子之間相互孤立,只有達到一定厚度時,才會形成連續的薄膜,此時其厚度可能已經超過了臨界厚度,并且金屬膜的電阻率與其表面粗糙度、殘余應力等也有很大關系,隨著表面粗糙度及殘余應力的增加而增大[23]。所以,為了使仿真中設置的Al薄膜的反射率與測試結果接近,需要確定等效的薄膜厚度deff,并用它代替實際薄膜的厚度dAl。通過大量的仿真計算,找到deff與dAl的對應關系,即確定厚度系數α,α=deff/dAl。
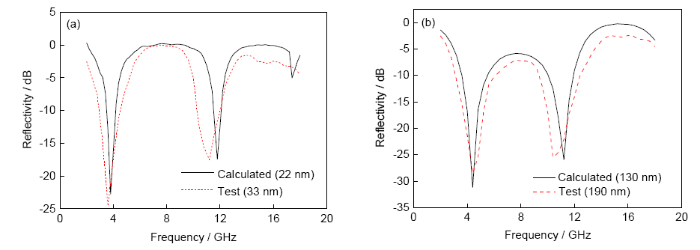
以8 mm的復合材料表面為Al薄膜為例(仿真模型見圖2b所示),確定厚度系數α。再由Al薄膜與復合材料組成的其它復合結構驗證該厚度系數α是否合理。采用磁控濺射方法制備不同厚度的Al薄膜,對不同厚度的Al薄膜與8 mm的復合材料的反射率進行測試。Al膜厚度設定為22 nm時的仿真計算結果與磁控濺射制備的33 nm的Al薄膜測試結果性能最接近,即α=deff/dAl≈0.7時,與測試結果擬合較好,如圖10a所示。可以看到,計算與測試的反射率最低點位置在低頻基本相同,高頻處有1 GHz的誤差,數值大小存在微小差別。本研究設計了另外一個金屬膜在介質中間位置的模型即Al薄膜放在8 mm復合材料的中間位置,計算了該模型的反射率,并與實驗結果對比,以驗證所設定厚度系數的正確性,如圖10b所示。計算結果與實測結果趨勢基本一致,反射率最低位置在低頻處基本相同,在高頻約有0.8 GHz的偏差,計算的反射率比實測值總體偏小,反射率峰值相差1.7 dB。計算中設定的薄膜厚度為130 nm,實際測試反射率的薄膜厚度約為190 nm,即α=deff/dAl≈0.7,與Al膜在復合材料表面結構所得到的系數α一致,確定了仿真計算與磁控濺射制備薄膜的α。
圖10 Al薄膜與8 mm復合材料的反射率計算與測試對比曲線
Fig.10 Curves of calculated and test reflectivities of 8 mm composite with an Al film in the cases of Al film being above the composite (a) and in the middle of the composite (b)
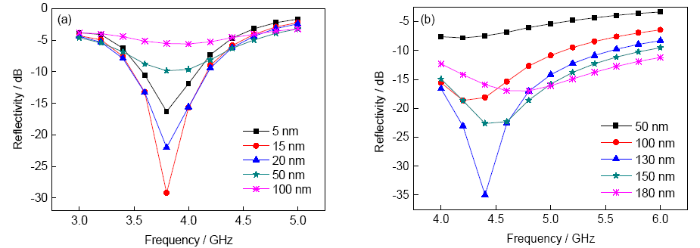
圖11a和b分別為不同厚度的Al薄膜位于8 mm復合材料表面及中間位置的仿真計算結果。圖11a中,Al薄膜厚度為5、15、20、50及100 nm時,對應的吸收峰值分別為-16.3、-29.2、-22、-9.8及-5.5 dB;Al薄膜為15 nm時,對電磁波的反射最小,之后隨著Al膜厚度的增加反射強度急劇增加;當厚度為100 nm時,復合結構對電磁波幾乎全反射。圖11b中,Al膜厚度為50 nm時對電磁波的反射很強,隨著厚度的增加對電磁波的反射逐漸降低,厚度為130 nm時達到最小反射后隨著厚度的增加,反射率逐漸增大,并且達到180 nm后反射率最低點位置出現了偏移。可見,Al薄膜的厚度直接影響Al膜與介質復合結構對電磁波的反射。2種復合結構的反射率不是隨著Al膜厚度單調增加或者減小,而是在一定厚度范圍內會出現較低的反射,并且結構不同其最小反射率對應的Al膜厚度也不同,對于一種結構存在著某一厚度的Al膜,復合結構對電磁波的反射最小。根據諧振吸收原理,電磁波在Al膜與介質復合結構中傳播的過程,實際上是振幅不同的多個波的往返傳播,當界面上的反射波與透射波進入介質經過一個來回后的幅值相等而相位相反時,反射為0。厚度不同的Al膜的阻抗不同,影響整個復合結構的輸入阻抗,根據傳輸線理論,其對反射率會產生影響。復合結構的反射率主要由Al膜決定,所以對Al膜厚度的計算尤為重要。
圖11 不同厚度Al薄膜在8 mm復合材料表面和中間位置的反射率仿真計算曲線
Fig.11 Simulation reflectivity curves of 8 mm composite with different Al films in thickness in the case of Al film being above the composite (a) and in the middle of the composite (b)
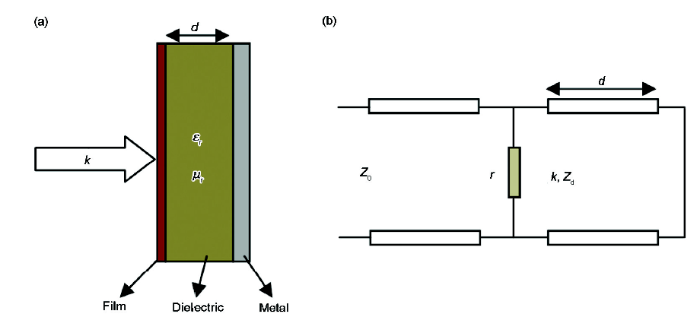
由金屬膜與單層介質材料構成的結構,其傳輸線等效電路模型如圖12所示。
圖12 金屬膜與介質復合結構示意圖及傳輸線等效電路模型
Fig.12 Metallic film and its corresponding dielectric composite structure (k—wave number in medium, d—dielectric layer thickness, Z0—wave impedance of air, Zd—wave impedance of dielectric, r—resistance)
該吸波結構的反射系數
式中,Z0為空氣的波阻抗,377。總的輸入阻抗Zin為:
式中,r為金屬膜的電阻,Zd為介質的輸入阻抗[25,26]:
式中,
將式(3)代入式(2)并化簡得:
當入射到復合結構的電磁波的反射為0時,
公式成立的必要條件為:
或
式(8)成立時,Zd=
將式(4)代入式(9)并化簡得:
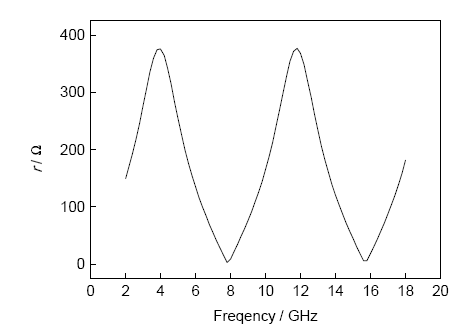
通過MATLAB進行求解,可以得到厚度為d的復合材料與金屬膜構成的復合結構反射系數為0時對應的Al膜的電阻。圖13為MATLAB求解得到的Al薄膜位于8 mm復合材料表面2~18 GHz反射率為0時對應的Al膜的電阻。通過式(9)可以得到電阻值與仿真計算中材料厚度的對應值,磁控濺射制備的金屬膜可以通過四探針法測得其電阻。這一計算方法同樣適用于金屬膜位于介質任意位置及金屬膜為頻率選擇表面時與介質復合結構發生諧振時的電阻,該方法為金屬膜與介質復合結構電磁性能的設計提供了重要方法。
圖13 8 mm復合材料與Al薄膜復合結構諧振時對應的Al膜電阻曲線
Fig.13 Resonant resistance (r) curve of 8 mm glass fiber reinforced plastic composite structure with Al film
對不同厚度的復合材料諧振時對應金屬膜電阻的求解,可以方便地得到具有較低反射率的復合結構。工程中利用數值模擬計算對復合結構的電磁性能進行輔助設計,可以縮短設計周期,節省設計成本,為工程設計提供方便。
(1) 通過大量的仿真計算與實際測試比對,確定了仿真計算中玻璃纖維增強樹脂基復合材料的等效電磁參數,介電常數實部εr=4.4,電損耗角正切tanδε=0.01,磁導率μr=1,磁損耗角正切tanδμ=0。
(2) Al薄膜與玻璃纖維增強樹脂基復合材料結構中Al薄膜的厚度對結構的反射率影響很大,確定了仿真計算中Al薄膜與磁控濺射制備Al薄膜的厚度系數α=deff/dAl≈0.7。
(3) 研究了Al薄膜與玻璃纖維增強樹脂基復合材料結構中Al薄膜的厚度與反射率的關系。根據傳輸線理論,利用公式推導及MATLAB求解,得到了超薄Al膜在8 mm玻璃纖維增強樹脂基復合材料表面發生諧振時最低反射率對應的Al膜的電阻。這種方法同樣適用于其它金屬膜為均勻膜或為頻率選擇表面時,在復合材料任意位置處發生諧振時對應的金屬膜的電阻值的求解。
 , 王晨
, 王晨
1 實驗方法
1.1 Al薄膜及玻璃纖維增強樹脂基復合材料的制備
1.2 平板反射率的測量
2 模型的建立
2.1 仿真流程
(a) metallic frequency selective surface and composite structure
(b) Al film and composite structure
2.2 等效電磁參數
Fiber
εr
tanδε
D glass fiber
4.0
0.002~0.003
Quartz fiber
3.8
0.0001~0.0002
Polyester resin
2.7~3.2
0.005~0.02
Epoxy resin
3.0~3.4
0.01~0.03
Glass fiber/epoxy
4.2~4.7
0.007~0.014
Glass fiber/polyimide
4.0~4.4
0.006~0.012
3 結果與分析
3.1 玻璃鋼復合材料等效電磁參數的確定
3.2 Al薄膜電磁參數的設定
3.3 Al薄膜厚度對反射率的影響
3.4 電路諧振時Al薄膜厚度計算
(a) sketch of the structure
(b) transmission line equivalent circuit model of this structure
4 結論
來源--金屬學報






 滬公網安備31011202020290號
滬公網安備31011202020290號
