分享:氫化空位的基本性質及其對金屬力學行為的影響
西安交通大學金屬材料強度國家重點實驗室 西安 710049
摘要
金屬和合金材料中廣泛存在著氫脆現象,即由于氫的滲入使得材料的塑性變形能力顯著下降,導致材料傾向于發生脆性或準脆性斷裂。盡管氫誘發材料失效的問題被研究了很多年,但微觀機理一直存在著廣泛爭議。本文以近年來的研究結果為基礎,提出了“氫化空位”的概念(即氫-空位復合體),認為其是氫致材料失效初期微觀結構的最小載體。利用多尺度模擬并結合實驗測試,揭示出氫化空位不同于空位的特殊性質,研究了氫環境下在塑性變形中氫化空位的產生、聚集并經過長時間演化形成納米孔洞的過程,構建出原子尺度事件與微觀失效之間的聯系。該研究豐富了對氫脆微觀機制的理解,同時氫化空位的概念也為揭示氫環境下的其它特殊力學行為提供了思路。
關鍵詞:
氫是金屬及合金中一種重要的點缺陷,通常以原子的形式存在于晶格的間隙位置。H的滲入會顯著地影響金屬材料的塑性行為,使材料具有脆性或準脆性斷裂的傾向,即氫脆現象[1,2]。氫脆最早被發現在鋼鐵材料中,隨后在很多金屬中都發現了類似的現象。氫脆問題涉及到石油輸運、建筑安全等諸多領域,如何抑制氫脆現象的發生一直是科學界和工業界的研究熱點。雖然氫脆的研究也從未間斷,但氫脆產生的微觀機理一直未能得到詳細而合理的解釋。
過去幾十年的系統研究提出了4種主要的氫脆機制,盡管它們都各自解釋了一定的氫脆現象,但同時也都表現出其局限性。(1) 氫化物的形成:實驗發現對某些金屬材料(如Nb),H的滲入能夠與金屬形成金屬氫化物,進而被認為是產生材料失效的主要原因[3]。但這一機制僅限于一些特定的VB族金屬元素,并不具有普適性。(2) 氫弱化金屬原子間結合力:該理論認為氫脆的原因是H偏聚在裂紋尖端的應力集中區,進而弱化了金屬鍵的結合能,從而促使金屬斷鍵而使得材料失效[4]。但相關理論表明,這種機制的發生需要H在裂紋尖端原子濃度比接近1。但通常情況下,氫脆現象在H平均濃度僅為10-5的情況下就會發生。因此,該理論起作用所需的高濃度氫環境能否達到仍存在廣泛質疑。(3) 氫加劇局部塑性變形:實驗發現氫環境下材料失效的斷裂面通常與位錯的滑移面是一致的[5],這表明材料的斷裂很可能是與位錯塑性變形緊密地聯系在一起。一些實驗和理論計算[6,7]表明,H的滲入能夠加劇位錯運動,從而顯著地增加材料局部的塑性變形行為,由此發展了氫加劇局部塑性變形的氫脆機理。但該理論無法從微觀上解釋由位錯滑移主導的塑性變形如何導致材料發生脆性斷裂。(4) 氫促進空位形成:最近有實驗[8,9,10]表明,氫環境下材料發生塑性變形后空位的濃度會顯著上升,結合其它一些實驗結果,該理論將誘發氫脆的原因歸結于過飽和的空位,而并非氫本身。但該理論仍缺乏微觀的證據和解釋。
深入理解材料的脆性或準脆性斷裂行為,一個核心問題是誘發材料失效的載體是什么?抑或說材料失效的初始階段中,對應的微觀行為是什么?從微觀層面上看,考慮到原子斷鍵的不可逆性,可以通過金屬鍵斷鍵的數量來定量地表征材料的失效程度。在塑性變形前,金屬的成鍵總數(M)具有最大值。以α-Fe為例,M=8N*/2,N*為體系總原子數。當材料發生金屬鍵斷鍵行為時(如產生了新的表面等),成鍵總數將會減少。而對于金屬鍵轉移的行為(如位錯滑移、孿晶界遷移等),成鍵總數在整個過程中是守恒的。因此,成鍵總數的變化可以作為定量衡量微觀反應的序參量,在宏觀尺度應用Griffith斷裂準則[11]之前,該序參量可以作為描述材料脆性或準脆性斷裂的一個判據。例如,孔洞的形成和長大、裂紋的萌生和擴展都是在經歷一個成鍵總數不斷減小的過程[12]。
成鍵總數描述了整個體系的斷鍵行為,但用來表征材料失效仍顯得過于粗糙,其無法在空間分布和濃度以及隨時間的演化等方面對材料的局部失效給予描述。在原子尺度上,空位可以被看作是塑性變形初始階段時材料發生失效的最小事件,例如,在α-Fe中一個空位的形成會導致成鍵總數減少8個。因此,材料的整體失效(即斷鍵總數的持續發生)可以等效地看作是空位不斷增殖和聚集的過程。通常,金屬塑性變形主要依靠位錯或孿晶來完成,在無氫的環境下空位對金屬失效的作用并不顯著。但在有氫的環境中這種狀況有可能被極大地改變,從而發生空位占主導的失效機制。
由于H的體積小且在金屬中具有非常強的擴散能力,同時實驗條件具有一定的局限性,因此僅依靠實驗很難追蹤和表征H是如何誘發材料脆性或準脆性斷裂,尤其是H在材料失效初期的行為。實驗條件的局限性大大降低了對這一問題的深入研究。最近幾十年興起的計算模擬技術給研究氫脆提供了新的途徑。原子模擬技術的發展和成熟使得人們能夠從原子層面上研究材料在外在條件下所發生的變化。對于當前的氫脆行為,計算模擬也能夠很好的輔助實驗,提供更多的微觀信息,從而有助于人們對這一問題的理解。
本文以作者課題組的研究結果為基礎,用多尺度的計算模擬技術(分子動力學(molecular dynamics,MD)、動力學蒙特卡洛(kinetic Monte Carlo,KMC)、團簇動力學(cluster dynamics))并結合實驗表征的方法,研究金屬α-Fe在氫環境下塑性變形過程中微觀結構的演化,提出了一個新的概念——氫化空位,即氫和空位的復合體。研究發現相比于空位,氫化空位在熱力學、動力學以及與位錯的相互作用上都具有較大差異,其很可能是氫脆現象中材料破壞的最小單位,在材料失效中扮演著重要角色。
H在完美的晶體α-Fe中存在于四面體間隙位置。前期的第一性原理計算[13,14]表明,當晶體中存在空位時,H在空位周圍具有比在四面體間隙中更低的能量。在金屬中一個空位可以與多個H原子結合,并形成熱力學上穩定的氫-空位復合體,這里稱之為氫化空位。氫化空位廣泛地存在于bcc和fcc結構的金屬體系中。單個空位與不同數量H原子的平均結合能Eb,其計算公式為:
式中,E表示體系能量。N和n分別為體系中Fe和H的原子數。
以α-Fe為例,一個空位最多可與6個H原子結合。如表1[15,16]所示,本課題組[16]利用分子動力學模擬所采用的嵌入原子模型(EAM),計算出氫化空位結合能,該模型與第一性原理計算的結果[15]吻合較好。
表1 金屬α-Fe中VaHn (n=1~6)的平均結合能[
Table 1 Averaged binding energy of VaHn (n=1~6) in α-Fe[
氫化空位不僅具有良好的熱力學穩定性,而且還具有較低的擴散速率。利用NEB (nudged elastic band)算法[17],可計算出不同類型的點缺陷(氫、空位和氫化空位)在α-Fe晶格中的遷移勢壘(Em),如圖1[16]所示。H的體積小,具有非常強的擴散能力,其擴散所需要克服的勢壘僅為0.04 eV。而空位的遷移勢壘則為0.64 eV。氫化空位相比空位更高,可達到0.76 eV,由此可見氫化空位相比于空位具有較低的擴散能力。利用擴散激活能,可進一步估算出擴散系數D=D0exp(-Em/(kBT)),其中D0為擴散常數,kB為Boltzmann常數,T為熱力學溫度。室溫下D0=2.76 cm2/s,空位和氫化空位的D分別為5.63×10-11和5.57×10-13 cm2/s。
圖1 氫化空位、空位和氫在α-Fe中的擴散激活能[
Fig.1 Migration paths of hydrogen-vacancy complex, vacancy and hydrogen in α-Fe. As indicated in red, blue and green lines, the migration barriers of corresponding point defects are 0.76 eV, 0.64 eV and 0.04 eV, respectively[
在實際材料內部,存在著各種類型吸收空位使其湮滅的不可動缺陷,如晶界、第二相析出物等。因此,空位或氫化空位在晶體中都有一定的存在時間(tlife),即點缺陷通過擴散到達這些吸收源所需要的時間。如果把擴散的自由程設為吸收源的平均尺度(Lsink),那么點缺陷的存在時間為tlife=
在金屬的塑性變形中,位錯通常是塑性應變的主要載體。位錯的運動及其與不同類型缺陷的相互作用將不可避免地影響材料的力學行為。利用原子模擬重點研究不同點缺陷(空位和氫化空位)與位錯之間的相互作用,將有助于進一步揭示出氫化空位的基本性質及其與空位的差異。在金屬α-Fe中構建一個a/2<111>類型的刃型位錯,室溫下在xz平面內施加切應力可驅動位錯在{110}滑移面上運動。通過在位錯滑移前方設置不同類型的點缺陷(空位、氫、氫化空位)來進一步研究他們與位錯的相互作用。
原子模擬發現,相比于空位,氫化空位與刃型位錯的相互作用行為完全不同。圖2a和b[16]比較了這兩類不同點缺陷(空位和氫化空位)在遇到刃型位錯時的相互作用。當位錯掃過空位時,空位是不穩定的,其會被刃型位錯“吸收”,在位錯線上形成一個空位割階。“吸收”空位后,位錯仍具有良好的遷移能力,可在滑移面上繼續移動。但氫化空位與刃型位錯的相互作用則完全不同,當位錯掃過氫化空位時,氫化空位表現得非常穩定,并對位錯產生一定的釘扎作用。即使位錯脫扎,氫化空位仍穩定在初始位置。氫化空位的穩定性可以進一步地通過氫和位錯對空位的“爭奪”能力方面表現出來。如圖2c[16]所示,盡管一個刃型位錯可以“吸收”空位,且攜帶空位一起運動,但遇到H原子時,氫能夠將割階空位從位錯上“奪”過來,并將空位以氫化空位的形式保留下來。而當位錯攜帶著割階空位遇見氫化空位時,氫化空位甚至能夠“奪”過割階空位而進一步長大,如圖2d[16]所示。在這里,刃型位錯充當著空位的輸運載體,幫助空位在氫化空位上聚集,從而通過滑移的方式實現了物質質量上的轉移,這種方式區別于空位通過擴散而實現聚集的傳統方式。
圖2 金屬α-Fe中,4個獨立的事件揭示出氫化空位與位錯相互作用后仍具有良好穩定性[
Fig.2 Four independent events illustrating the high stability of hydrogen-vacancy complex when interacting with dislocations in α-Fe. Crystals are oriented along x-[111], y-
以上研究了氫化空位的基本性質(熱力學穩定性、動力學特性)及其與位錯的相互作用。接下來,以金屬α-Fe為例,通過分子動力學模擬研究氫環境下空位及氫化空位在塑性變形中的演化,進而揭示出其對力學行為的影響。原子模擬的空間尺度約為23 nm×23 nm×23 nm (總原子數超過106)。周期性邊界條件施加在x、y、z 3個方向。構建了兩種不同類型的初始位錯構型。構型I中含有4個對稱分布的a/2<111>類型的棱柱形位錯環,如圖3a[16]所示。構型II中含有4個a/2<111>/{110}類型的切變位錯環擴展形成的位錯網絡,如圖3b[16]所示。初始位錯構型創建后,在體系中進一步引入隨機分布的H原子。實驗中,H在Fe或鋼中的含量較低,其原子濃度一般為10-5~10-3量級[8,10]。但是,氫誘發的材料失效通常發生在高應力區,在該區域中,H的含量要明顯高于平均濃度。為了涵蓋實驗中H濃度的范圍,模擬中H的濃度控制在10-4~10-2。引入H原子后在室溫下對體系弛豫一定時間使得H擴散達到平衡。最后沿x方向施加單向拉伸,初始構型I和II的拉伸方向分別為[100]和[011],最大應變為60%。
圖3 2個穩定的初始位錯構型[
Fig.3 Stable dislocation configurations of prismatic loops (PLs) (a) and dislocation network evolved from shear loops (SLs) (b). Spheres with blue and gold color refer to the iron atoms in dislocations and vacancies, respectively[
模擬發現,位錯自身運動以及位錯之間的相互作用會產生大量的空位。空位的產生方式主要有4種[18],包括棱柱形位錯的擴展、割階的非保守運動、螺型位錯的交滑移以及位錯-位錯的相互作用。不同方式產生的空位都有其各自特點,使得空位在空間的分布或隨機或有序,或單一或多個。傳統的觀點認為位錯既是空位的產生源,也是空位的吸收源。但是,在氫環境中,當空位以氫化空位的形式被穩定后,位錯作為吸收源的作用將被明顯削弱。因此,氫的存在改變了位錯產生和吸收空位的偏向性。
圖4a[16]顯示了空位和氫化空位總濃度CV (≡CVa+CVaHn)隨外加應變(ε)在不同氫濃度(CH)下的變化。以位錯構型I為例,當CH (=10-4~10-3)接近或小于CV時,CV呈類似指數形式的增長并逐步趨于飽和;而當CH(=10-2)大于CV時,CV呈現出近似線性的增長。CV在不同CH條件下的變化主要取決于氫化空位在體系中所能達到的濃度。如圖4b[16]所示,對于CH>CV,CVaHn能夠達到CV的數量級,表明在塑性變形中,絕大部分產生的空位都以氫化空位的形式穩定存在。而當CH降低時,大部分的空位由于缺少H的“保護”,很容易被位錯“吸收”而湮滅。
圖4 不同氫濃度(CH)下,空位和氫化空位的總濃度(CV≡CVa+CVaHn)和氫化空位濃度(CVaHn)隨應變(ε)的變化[
Fig.4 Variation of concentration of vacancies and hydrogen-vacancy complexes (CV≡CVa+CVaHn) (a) and concentration of hydrogen-vacancy complexes (CVaHn) with applied strain (ε) (b) under different hydrogen concentrations (CH) in iron. CV, CVa, CVaHn and CH are in the units of atomic ratio[
上述模擬發現,當CH=10-2 (遠大于CV)時,CV表現出一個線性增長的趨勢。由于H在金屬中具有極高的擴散速率,絕大多數的空位都會被H以氫化空位的形式穩定下來而不容易湮滅,該條件下的空位可認為接近于過飽和的上限濃度。下面將構建力學模型對此線性增長給予描述。CV的凈增長率可表示為dCV/dt=Π -η,其中Π為空位濃度的產生率,η為空位濃度的消失率[19]。當CH>CV,空位的湮滅率非常低,η可近似地認為趨于0,進而dCV/dt=Π。而
式中,χ為無量綱的參數,Ω0為原子體積,σ為流變應力,
式中,C0為初始空位濃度,系數K為σ的函數,即K(σ)=χΩ0σ/Qf。由此得到依靠理論模型,預測出K(σ)的數值分別為11.76×10-3 (位錯構型I)和20.24×10-3 (位錯構型II)。而在當前模擬中,通過在塑性區對其做線性擬合,得到2種位錯構型中K(σ)的數值分別為3.93×10-3和3.50×10-3,如圖5[16]所示。對比分析表明,模擬數值和理論數值在同一數量級。數值差異主要源于理論模型采用的是在較高溫度下(0.5Tm)的系數χ,但當前的模擬溫度則是室溫。
圖5 在CH=10-2條件下,2個體系的應力-應變曲線及CV隨ε的變化[
Fig.5 Stress-strain (σ-ε) curves of uniaxial tension for both systems containing SLs and PLs under CH=10-2 (a), and variation of concentration of CV, including both unhydrogenated vacancies and hydrogen-vacancy complexes (b). The yellow and cyan solid lines are the linear fit to the two curves in strain range 0.06~0.6 [
通常在純金屬中空位的熱力學平衡濃度在室溫或較低溫度下非常低,只有當溫度升高到接近熔點時,其平衡濃度才會顯著地上升,原子比可達到10-4~10-3 [21]。本文的原子模擬發現,氫環境下,由于氫化空位具有較好的熱力學穩定性以及較低的遷移率,使得塑性變形中CV能夠極大的偏離平衡濃度,其數值可達到純金屬在接近熔點時的空位平衡濃度。需要強調的是,這種過飽和濃度只有在有H的環境中才能出現。無氫的環境下,由于缺少氫的保護,塑性變形產生的空位將隨時間湮滅而最終趨向于平衡濃度[22]。
如前所述,單個空位可看做是材料失效的最小載體或晶體中自由體積的最小單位。在很多情況下,金屬材料的失效通常發生在大量金屬斷鍵或產生高密度自由體積的條件下,如高溫蠕變[18]、材料經輻照后孔洞的形成和聚集[23]或超大變形后微觀結構的演化[24,25]等。在當前含H的體系中,空位濃度具有極高的數值(CV≈10-3),其等效于金屬斷鍵總數與成鍵總數的比例高達10-3數量級,因此將和上述幾種情況一樣,對材料的力學行為具有重要的影響。
但由于原子模擬的時間尺度非常短(通常在納秒級別),一些需要較長時間激發的行為(如空位及氫化空位的擴散等)是無法體現的。為了探索過飽和空位/氫化空位在大時間尺度的擴散行為,利用KMC[26,27]方法進一步研究一定量隨機分布的氫、空位和氫化空位的動態演化過程。為了簡化計算,本工作創建了一個二維模型,初始空位/氫化空位濃度接近于上述塑性變形誘發的過飽和濃度,利用原子模擬計算得出不同類型點缺陷的擴散激活能以及結合能。如圖6所示,初始隨機分布的點缺陷通過擴散將慢慢聚集為小的點缺陷團簇。H與空位傾向于形成氫化空位,經過長時間的演化,空位慢慢聚集在氫化空位的周圍。氫化空位作為一個穩定的核心,能夠吸收更多的H和空位,從而實現空位的聚集。
圖6 動力學Monte Carlo模擬空位/氫化空位的聚集過程
Fig.6 The accumulation of vacancy and hydrogen-vacancy complexes by diffusion in kinetic Monte Carlo simulations. Spheres with gold and black colors refer to vacancies and hydrogen. Taking hydrogen-vacancy complexes as nuclei, vacancies are accumulated as indicated by the red circles (t—time)
為了進一步揭示空位/氫化空位在更大時間和空間尺度內的演化,本課題組發展了基于平均場理論[28]和分組數值計算[29]的團簇動力學方法(相關的算法以及模型參數設置詳見文獻[16])。初始條件為:CVa=10-6,CH=10-4,
圖7 團簇動力學模擬室溫下團簇尺寸分布隨時間的變化[
Fig.7 Mean radius distributions of proto nano-voids at different ageing time at room temperature by using cluster dynamics simulations. As time increases, the most probable size of cluster increases, indicating the accumulation of vacancies and hydrogen-vacancy complexes during long-time evolution[
本文同時開展了實驗測試以對上述多尺度模擬給予一定支持。選擇X65和X80類型管線鋼,滲入一定量的H (1×10-6~4×10-6,質量分數),施加拉伸變形直到材料失效斷裂。變形后試樣的晶粒尺寸從1~3 μm減小到20~50 nm,這是由于位錯主導的塑性變形導致了晶粒細化。利用聚焦離子束(FIB)切出斷口上的薄層,通過透射電子顯微鏡(TEM)觀察薄層中的微觀組織,如圖8[16]所示。發現氫脆破壞的管線鋼斷口下面的位錯密度非常高,其誘發出一個大的塑性變形區[30]。在斷面上能夠清晰地看到一系列高密度、高低不平的淺坑,其尺寸深約1~5 nm,寬5~20 nm。這些高密度的淺坑表明管線鋼發生了準脆性斷裂,而淺坑的形成源于材料內部納米孔洞的萌生[30]。納米孔洞基于上述模擬所揭示出的氫化空位主導的機制形核并長大。
圖8 實驗中在管線鋼中觀察到的氫脆現象[
Fig.8 Experimental observations on hydrogen embrittlement in steel[
其它一些實驗也對塑性變形中氫化空位對力學行為的影響提供了更多的間接支持。利用正電子湮滅實驗,在不同金屬和合金中(如Fe、Ti等),都發現H的存在會有效地增加空位濃度以及空位團簇的形成[31],這與上述模擬結果是一致的。此外,利用正電子湮滅的測試還發現,平均正電子壽命在靠近斷口表面的區域會增加,該實驗認為H的存在會促進空位的形成和聚集,這些空位團簇是微觀結構破壞的主要原因[9,32]。而對滲氫的鐵或鋼進行力學變形后,關閉氣源繼續再卸載,發現微觀結構的破壞仍在累積,其失效程度與氫環境下一致,該實驗推測氫化空位是引發失效的主要原因[10]。以上模擬也表明,氫化空位具有良好的穩定性,過飽和的氫化空位濃度能夠保持較長時間,該實驗也側面支持了模擬結果。此外,對X70管線鋼的力學測試發現,滲氫條件下在擴展的疲勞裂紋尖端附近,塑性區的尺寸要大于沒有滲氫的樣品,同時也推測出生長的疲勞裂紋周圍高塑性變形區出現了氫化空位的聚集以及納米孔洞的形成[33]。
基于以上的模擬和實驗結果,本工作梳理出一個在力學變形中,由氫化空位主導的在材料失效初期的機制。在一個應力集中區域(如裂紋尖端),H的滲入能夠顯著增加該區域的塑性變形,由此引發的位錯運動以及位錯-位錯之間的相互作用會誘發大量的空位。而氫環境下,氫通過擴散快速與空位結合,形成穩定的氫化空位。由于大量空位的穩定存在,使得局部區域的空位/氫化空位的濃度能夠達到一個過飽和的狀態。隨著應變和時間的累加,氫化空位作為核心將吸收更多的空位聚集長大,并形成納米孔洞,在應力作用下將進一步促使孔洞的長大和合并,最終導致材料失效。考慮到氫化空位在金屬和合金中廣泛存在,氫化空位的概念以及對力學行為的影響作用對其它體系也具有適用性。
不僅在氫脆領域,利用氫化空位還可以進一步理解和揭示其它體系以及領域中特殊的力學行為。實驗發現在金屬Al中H的存在會對位錯產生釘扎效應,但奇怪的是,釘扎所需要的時間遠超過氫擴散的弛豫時間[34]。利用原子模擬發現對位錯起釘扎作用的不是H原子本身,而是氫化空位,因此具有較長的弛豫時間和更強的釘扎作用[34],從而合理解釋了金屬Al中位錯的特殊運動行為,也在其它體系進一步證實了氫化空位的存在。氫化空位不僅僅對位錯主導的塑性變形有影響,對Ni基合金的研究發現,合金化會降低空位以及氫化空位在孿晶界上的形成能,從而促進納米孔洞的形成以及裂紋在孿晶界處的萌生[35]。此外,氫化空位還用來進一步解釋金屬Al在高溫下界面結構的演化。實驗發現,利用電子束滲氫的過程中在金屬內部會形成大量過飽和空位,氫與空位結合形成穩定的氫化空位,在臨界溫度150 ℃下,這些氫化空位相對穩定,但當溫度超過臨界溫度,氫化空位分解,并快速擴散到界面處進而破壞金屬-氧化物界面,導致Al-Al2O3界面處形成巨型空腔[36]。
針對金屬和合金中廣泛存在的氫脆現象,本文提出了“氫化空位”的概念(即氫-空位復合體),用于理解氫環境下的一些特殊力學行為。利用多尺度模擬并結合實驗測試,研究發現氫化空位在熱力學和動力學方面有著區別于空位的特殊性質。相比于空位,氫化空位具有良好的熱穩定性,同時具有較低的遷移速率,因此很難通過擴散而湮滅。氫化空位與位錯相互作用后非常穩定,對位錯有很強的釘扎作用。對金屬Fe在室溫的塑性變形發現,位錯的運動及相互作用可產生大量空位,而在氫環境下,氫通過擴散與空位結合形成穩定的氫化空位,使得材料中空位/氫化空位的濃度處于過飽和狀態,大變形下其濃度接近于純金屬在溫度接近熔點時的平衡空位濃度。經過長時間演化,氫化空位通過不斷捕獲空位聚集最終會形成納米孔洞,在應力的作用下孔洞合并并擴展,最終導致材料的失效。
氫化空位是氫環境下微觀結構破壞的最小載體,可看作氫脆現象中材料失效初期的基本單位。而且,氫化空位對力學行為的影響不僅僅限于當前研究的α-Fe,對于其它金屬(如Al和Ni等)也具有普適性。本文的研究進一步豐富并加深了對氫脆微觀機制的理解,所提出的氫穩定空位并促進納米孔洞形成的機制,是除了較早的機制外,氫引發材料失效的一種新機制。
在本文的基礎上,借助于氫化空位的概念,還進一步解釋了Al中位錯在氫環境下的特殊運動行為以及金屬-金屬氧化物在高溫下界面失效的問題,同時氫化空位的概念也有助于理解氫環境下Ni基合金在孿晶界處空位的聚集以及納米孔洞的形成。
今后的工作一方面將繼續探索氫化空位對力學行為的影響,如氫化空位在裂紋尖端的聚集以及對裂紋萌生以及擴展的作用。另一方面,也將借助于氫化空位的概念來理解其他領域的科學問題,如核材料中氦與空位的結合及其對力學行為的潛在影響。
1 氫脆現象中材料失效的最小載體
2 氫化空位的基本性質
2.1 氫化空位的熱力學穩定性
Method
VaH
VaH2
VaH3
VaH4
VaH5
VaH6
MD[16]
0.603
0.603
0.425
0.346
0.217
0.158
DFT[15]
0.559
0.612
0.399
0.276
0.335
-0.019
2.2 氫化空位的動力學特征

3 氫化空位與位錯的相互作用

(a) when a a/2<111>-type edge dislocation interacts with a vacancy in the slip plane, the dislocation absorbs the vacancy
(b) in contrast, the hydrogen-vacancy complex is very stable when colliding with an edge dislocation
(c) the stability of hydrogen-vacancy complex is further confirmed when lattice hydrogen grabs an absorbed vacancy from an edge dislocation and stabilizes it in the form of a hydrogen-vacancy complex
(d) the hydrogen-vacancy complex can even grow displacively by capturing more vacancies that were absorbed by edge dislocations
4 氫化空位在塑性變形中的產生與增殖
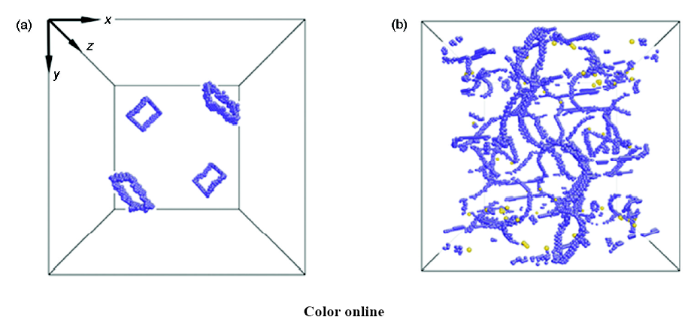


5 氫化空位的聚集

(a) t=0 s (b) t=0.002 s (c) t=0.021 s (d) t=0.188 s

6 實驗觀察以及對氫脆現象的啟示
6.1 納米孔洞的實驗觀察

(a) TEM image of deformation microstructure underneath a hydrogen embrittled quasi-brittle fracture facet in a tensile tested X65 grade pipeline steel
(b) SEM image of a typical hydrogen embrittled quasi-brittle fracture surface of X80 grade steel fracture toughness tested in 3000 psi H2 gas pressure
6.2 氫化空位的其它實驗支持
6.3 基于氫化空位機制的失效過程
7 氫化空位在其它領域的推廣
8 結論與展望
來源--金屬學報







 滬公網安備31011202020290號
滬公網安備31011202020290號
