分享:SiC/2009Al復合材料的變形加工參數的優化仿真研究
對粉末冶金法制備的15%SiC (體積分數)/2009Al復合材料熱變形參數的仿真優化方法進行了探討。通過熱壓縮實驗獲得復合材料的動態真應力-真應變曲線,由此建立了最大應變量下應變速率敏感指數(m)分布圖。在不同m值對應的變形參數下,對復合材料的熱壓縮過程進行有限元模擬,分析了熱壓縮樣品的流變應力、應變、危險系數分布等,結合微觀組織驗證了以m作為評價復合材料加工參數依據的可靠性,并由此確定15%SiC/2009Al復合材料的最佳熱變形參數所對應的變形溫度和應變速率分別為500 ℃和0.01 s-1。
關鍵詞:
本工作通過熱壓縮實驗,獲取了15%SiC (體積分數)/2009Al復合材料在不同變形參數下的流變應力-應變曲線,并基于此數據構建了應變速率敏感系數(m)隨工藝參數變化分布圖,選取不同m所對應的變形參數進行了變形加工有限元模擬,驗證了依據m演化作為優化變形工藝參數的可靠性,并對不同加工參數下該復合材料的成形能力進行了評價。
實驗材料為真空熱壓燒結制備的15%SiC/2009Al復合材料。基體為Al-4.5Cu-1.6Mg (質量分數,%)。其制備過程如下:首先將SiC顆粒(平均粒徑7 μm)和鋁合金粉末(平均粉末粒徑13 μm)按比例機械混合6 h,將顆粒和粉末的混合體進行冷壓,然后將冷壓坯放入真空熱壓爐中經除氣、熱壓燒結成復合材料坯錠。
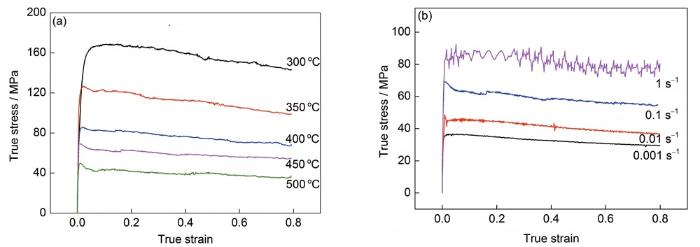
將熱壓錠加工成直徑8 mm×12 mm的圓柱壓縮試樣,試樣兩端車平,表面光滑無缺陷。使用Gleeble-3800熱模擬試驗機進行熱壓縮實驗,變形溫度分別為300、350、400、450和500 ℃,應變速率為0.001、0.01、0.1和1 s-1,每個試樣的最終應變量為0.8 (真應變)。為了減小高溫壓縮過程中試樣端面摩擦力對應力狀態的影響,在試樣與試驗機壓縮砧子之間加石墨片進行潤滑。進行熱壓縮之前,試樣以10 ℃/s的速率加熱到預定變形溫度,并保溫10 min,試樣溫度均勻后進行壓縮實驗。壓縮后的顯微組織通過DMI8 M光學顯微鏡(OM)進行表征。
有限元模擬基于DEFORM-3D商用有限元模擬軟件,將熱壓縮實驗所獲得的應力-應變數據導入材料庫中進行模擬。模擬的幾何模型如圖1所示。采用軸對稱模型,坯料原始尺寸為直徑8 mm×12 mm,為了節省計算時間,選取試樣的1/4進行模擬。采用DEFORM-3D軟件中自帶的四面體網格劃分器對坯料進行網格劃分,網格數量為20000個,網格單元的最大與最小尺寸比值設為1。在模擬熱變形過程中,網格的形貌會發生畸變,在此設定當網格畸變達到初始狀態的0.7時進行網格的重劃分,以確保模擬數據的準確性。坯料試件設為剛塑性體,在熱加工過程中上下模具的變形不計,設為剛性體。坯料與上下模具之間摩擦系數均設為0.3[22]。在模擬過程中將試件的溫度設為恒定不變。真應變量和應變速率根據模具下壓量與下壓速率確定。真應變計算公式如下所示:
圖1 有限元模擬幾何模型
Fig.1 Geometric model of finite element simulation
(a) sample model (b) assembly model of compression
式中,
圖2 15%SiC/2009Al復合材料的真應力-真應變曲線
Fig.2 True stress-true strain curves of 15%SiC (volume fraciton)/2009Al composite at 0.1 s-1 (a) and 400 ℃ (b)
應變速率敏感系數m是描述材料塑性變形能力的重要參數,一般材料的塑性越好,m也越高[9]。m可通過如下方程確定:
式中,
圖3 15%SiC/2009Al復合材料的應變速率敏感系數(m)隨變形參數的分布
Fig.3 Map of strain rate sensitivity (m) for 15%SiC/2009Al composite
顯然,當
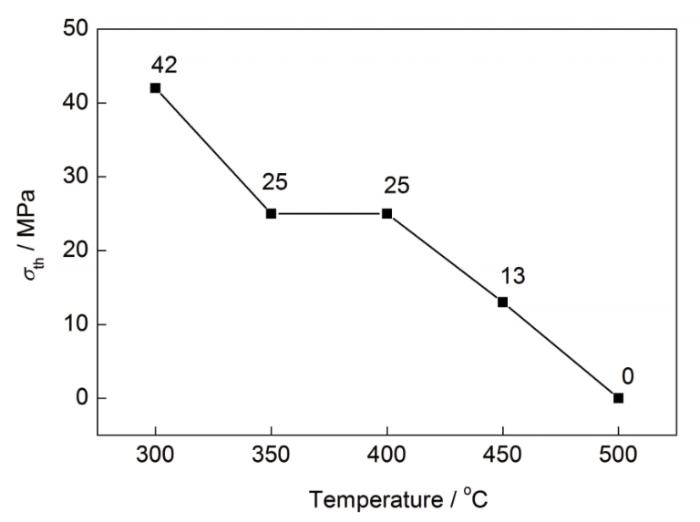
為了進一步理解m隨變形工藝參數變化的原因,采用Lagneborg-Bergman方法確定不同變形溫度下的
圖4 15%SiC/2009Al復合材料的門檻應力(
Fig.4 Variation of threshold stress (
2.3.1 應力、應變場分布
采用與最高、較高、最低m相對應的3個變形條件進行壓縮模擬,最高m為0.234,對應的變形參數為:500 ℃、0.01 s-1;最低m為0.105,對應的變形參數為:400 ℃、0.01 s-1;較高m為0.202,其對應變形參數為實驗所使用的最高溫度和最低應變速率:500 ℃、0.001 s-1,相應的變形過程中流變應力最低,以評價在對設備噸位要求最低情況下復合材料的變形工藝性。所有試樣的壓縮變形控制為真應變為0.8,經式(1)計算可得,模具最終下壓量為6.608 mm。
圖5a~c為3種變形參數下模擬得到的等效應力分布。可以發現,試樣的平均等效應力水平隨溫度的升高或應變速率的降低而減小,與m的大小無關。試樣內部的等效應力分布存在區別:對500 ℃和0.01 s-1 (最高m)下變形的試樣,其最高等效應力區域為試樣中心,且等效應力場變化較緩和。對500 ℃和0.001 s-1 (較高m)下變形的試樣,平均等效應力為所模擬的3種變形參數中最低,其最高等效應力區為與模具相接觸的上下端面。這是因為該變形參數下材料的平均等效應力較低,相比之下,試樣與模具相接觸的表面所產生的摩擦力區成為了高應力區。對400 ℃和0.01 s-1 (最低m)下的試樣,其最高等效應力區為試樣的拐角處,表明該參數下變形時試樣形狀突變區的應力集中現象較為嚴重。
圖5 15%SiC/2009Al復合材料在不同變形參數下的等效應力場、最大主應力場和等效應變場分布圖
Fig.5 Effective stress distributions (a~c), maximum principal stress distributions (d~f) and effective strain distributions (g~i) under different deformation parameters for 15%SiC/2009Al composite
Color online
(a, d, g) 500 ℃, 0.01 s-1 (b, e, h) 500 ℃, 0.001 s-1 (c, f, i) 400 ℃, 0.01 s-1
圖5d~f為3種變形參數下的最大主應力分布情況。可以發現,在試樣的腰鼓部位均出現最大主應力最高值,該部位處于拉應力狀態,因此壓縮過程的腰鼓部位將是最容易開裂的位置。盡管與模具相接觸的上下端面在變形過程中會向圓周外圍方向發生擴展,但在模具摩擦力的作用下仍處于壓應力狀態。
圖5g~i為3種變形參數下的等效應變分布情況。可以發現,試樣的心部和邊角處的等效應變最大,表明這兩處區域的變形量最大,而試樣的側面和端面的等效應變較小,尤其是端面的中心部位的等效應變最小,這是由于該處受到上下模具摩擦力的影響最為嚴重,材料的自由運動受到了限制。
為了對比3種變形參數對等效應變分布的影響情況,分別建立了等效應變量從上端面中心至下端面中心的數值變化關系(圖6a),以及等效應變從試樣中心至腰鼓處的數值變化關系(圖6b)。可以發現,變形參數為500 ℃、0.01 s-1的試樣最大應變量為1.140,在所示3種變形參數中最大應變量最小,應變梯度最小。表明該參數下試樣內部變形最均勻,而變形參數為400 ℃、0.01 s-1的試樣最大應變量為1.429,在所示3種變形參數中最大應變量最大、應變梯度最大,表明該參數下試樣內部變形均勻性最差。變形參數為500 ℃、0.001 s-1的試樣的變形均勻性介于其余2種變形參數之間。結合不同變形參數的模擬結果可以發現,等效應變分布與m的大小對應關系明顯,即m越大,抵抗局域化變形能力越強,等效應變梯度越小。從控制材料變形均勻性角度,應采用最高m對應的變形參數。對本研究所采用的復合材料,500 ℃、0.01 s-1下組織應該最均勻。
圖6 15%SiC/2009Al復合材料不同變形參數下的等效應變量隨試樣位置變化
Fig.6 Variations of effective strain with specimen locations from the center of the upper end to the center of the lower end (a) and from the center of the sample to the bulge (b) under different deformation parameters for 15%SiC/2009Al composite
2.3.2 變形損傷
為了檢驗不同變形參數下材料損傷的響應,采用通用的Cockcroft-Latham準則對該復合材料在熱壓縮過程中的損傷情況進行預測。該準則可用下式表達[33]:
式中,D為塑性變形危險系數,
圖7a~c所示為當真應變為0.8時,變形參數分別為500 ℃、0.01 s-1,500 ℃、0.001 s-1和400 ℃、0.01 s-1的
圖7 15%SiC/2009Al復合材料壓縮變形時的危險系數(D)
Fig.7 Distributions of damage coefficient (D) under the deformation parameters of 500 ℃, 0.01 s-1 (a), 500 ℃, 0.001 s-1 (b), 400 ℃, 0.01 s-1 (c) for 15%SiC/2009Al composite and curves of damage coefficient vs coordinate from the center to the bulge of the sample (d)
Color online
2.3.3 組織形貌驗證
圖8所示為壓縮真應變為0.8時,與最低m、最高m相對應的變形參數下的試樣中心部位與腰鼓部位的組織形貌,其中黑色顆粒為SiC,白色基底為SiC貧瘠區。2種變形參數下均未出現宏觀開裂等組織損傷,這是因為樣品的壓縮變形程度較低:由有限元模擬的危險系數分布可知,即便在最低m下的變形參數進行壓縮,當真應變為0.8時,其最大危險系數也小于0.25。進一步對SiC在基體中的分布情況進行觀察可以發現,最低m變形參數下中心部位SiC貧瘠區的尺寸明顯要小于腰鼓部位,而最高m變形參數下中心部位SiC貧瘠區尺寸與腰鼓部位相差較小。試樣不同部位的SiC分布差異性與變形均勻性有關。根據有限元模擬結果,最高m變形參數下中心區的最大等效應變為1.140,是腰鼓部位最小等效應變的1.762倍。而最低m變形參數下中心區的最大等效應變為1.429,是腰鼓部位最小等效應變的2.468倍,兩區域之間的等效應變差異相比于最高m增加了40.1%。由于最低m的樣品中心區的應變分量更大,該區域內的SiC貧瘠區的晶內變形將更嚴重,導致與腰鼓部位的SiC貧瘠區的尺寸形成較大的差別。綜上所述,采取最高m相對應的變形參數進行塑性加工,將減小SiC在不同部位的分布差異性。這驗證了有限元模擬結果:高m相對應的變形參數有利于促進樣品均勻變形。
圖8 15%SiC/2009Al復合材料壓縮變形試樣中的SiC分布
Fig.8 Distributions of SiC at variant locations with different m for 15%SiC/2009Al composite
(a) at the center part with the lowest m
(b) at the waist drum part with the lowest m
(c) at the center part with the highest m
(d) at the waist drum part with the highest m
2.3.4 最優參數下的單次可變形量評估
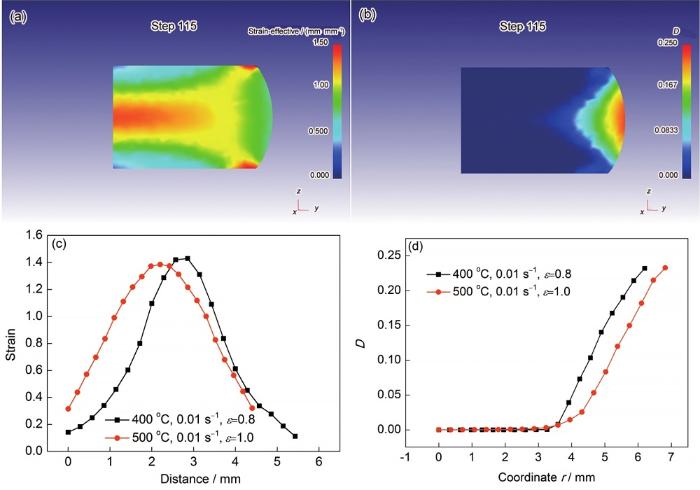
零件塑性加工過程中,為避免單次變形量過大造成損傷,通常需要多次變形與退火以達到最終所需的形狀。通過優化變形參數可以提高單次變形量,從而提高效率,并減少保溫過程中造成的能源消耗。從目前的研究結果可知,變形參數為500 ℃、0.01 s-1下,內部變形較均勻,且相同應變下最大危險系數最低,因此是最佳塑性變形參數。為了定量比較不同變形參數下的單次可變形量,在500 ℃、0.01 s-1下對樣品進行壓縮模擬,直至樣品的最大危險系數與400 ℃、0.01 s-1、真應變為0.8時的樣品相持平。最終模擬結果如圖9所示,試樣被壓縮的距離為7.6 mm,所對應的真應變為1.0,相對于變形參數為400 ℃、0.01 s-1,其單次可變形量增大了25%。
圖9 15%SiC/2009Al復合材料變形參數為500 ℃、0.01 s-1、真應變(ε)為1.0時的危險系數模擬結果
Fig.9 Simulation results of damage values for 15%SiC/2009Al composite at 500 ℃, 0.01 s-1 and the true strain (ε) of 1.0
Color online
(a) effective strain distribution
(b) damage coefficient distribution
(c) curves of effective strain vs distance from the upper end to the lower end along the center of the sample
(d) curves of damage coefficient vs coordinate from the center to the bulge of the sample
為了對比2種變形條件對等效應變分布的影響情況,建立了從上端面中心至下端面中心等效應變的變化曲線,如圖9c所示。可以發現,變形參數為500 ℃、0.01 s-1、真應變為1.0的樣品的最大等效應變值為1.385,要小于變形參數為400 ℃、0.01 s-1、真應變為0.8的樣品的最大等效應變(1.429)。以試樣的中心向腰鼓的最大位置做連線,繪制危險系數在試樣中心平面區域沿半徑的變化,如圖9d所示。可以發現,兩者達到相同最大危險系數的部位均處于腰鼓最大位置,真應變為1.0的樣品由于受到較大的宏觀變形,其中心與腰鼓最大處的距離有所增大。該部分結果表明,通過采用500 ℃、0.01 s-1的變形參數能夠有效地增大零件單次可變形量,這對提高加工效率具有重要意義。
(1) 根據15%SiC/2009Al復合材料的流變應力,建立了應變速率敏感系數分布圖,當變形參數為500 ℃、0.01 s-1時,應變速率敏感系數m達到最高值;變形參數為400 ℃、0.01 s-1時,m達到最低值。
(2) 使用有限元軟件對不同變形參數下復合材料的加工過程進行模擬,發現材料流變均勻性隨著m的升高而升高,變形危險系數隨著m的升高而下降。
(3) 分別在最高與最低m相對應的變形參數下對樣品進行壓縮變形模擬,發現當最大危險系數達到相同值時,最高m變形參數下的樣品的單次可變形量較最低m可提升25%。
1 實驗方法
圖1

2 實驗結果與分析
2.1 流變應力-應變曲線
圖2
2.2 應變速率敏感系數的變化
圖3
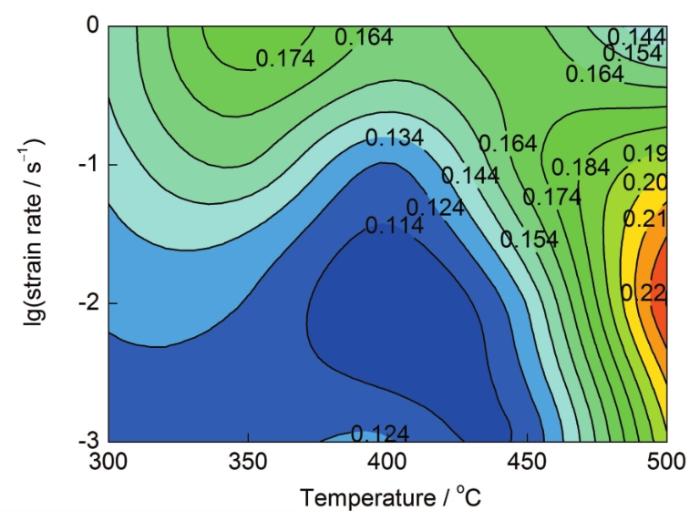
圖4
2.3 熱變形過程的有限元模擬與驗證
圖5

圖6
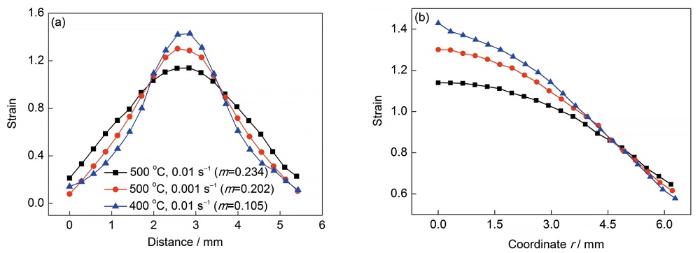
圖7
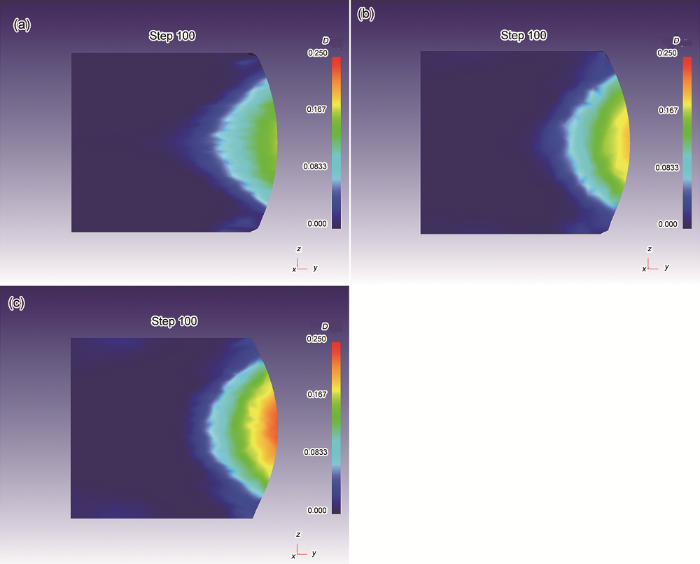
圖8

圖9
4 結論
來源--金屬學報







 滬公網安備31011202020290號
滬公網安備31011202020290號
