分享:Mn和In添加對SmCo7結構穩定性及磁矩影響的第一性原理計算
基于構建適用于第一性原理計算、原子比例準確為Sm∶Co = 1∶7的晶體結構模型,依據實驗研究中得到的物相共存結果,對Mn和In摻雜的Sm-Co體系模型進行了系列計算分析。利用熱力學計算方法,定量化研究了Mn和In在Sm-Co體系中優先占位特點及摻雜元素占位概率隨溫度的變化規律。通過Sm-Co合金摻雜體系的能量和電子結構計算,研究了Mn和In單摻雜SmCo7體系的結構穩定性。基于計算結果揭示了Mn和In對摻雜合金體系中原子間相互作用的影響,闡明了提升體系結構穩定性的微觀機制,并提出了Mn添加可增加SmCo7合金的總磁矩,揭示了摻雜元素對SmCo7合金飽和磁化強度的影響規律。
關鍵詞:
隨著航空航天、電動汽車技術的迅速發展,相關領域對具有高的磁性能且使用溫度更高的新型永磁合金提出愈加迫切的要求。已有的商業化永磁合金中,高溫磁性能最好的是Sm2Co17型永磁體,但其矯頑力仍然隨溫度升高而急劇下降,最高使用溫度一般小于350℃;而開發先進的高溫高性能磁體的目標是把使用溫度提高到400~550℃[1~3]。在Sm-Co型永磁材料中,具有TbCu7結構的SmCo7合金的磁晶各向異性場是Sm2Co17合金的1.2~1.4倍,其內稟矯頑力溫度系數也較低[4],相對于其他Sm-Co型合金,SmCo7合金具有更突出的高溫磁性能的開發潛力。然而,亞穩相SmCo7 (1∶7H)易分解為SmCo5 (1∶5H)和Sm2Co17 (2∶17R)雙相組織[5],很大程度上影響SmCo7的高溫磁性能,限制其實際應用。因此,深入研究SmCo7亞穩相的穩定性及其轉變規律,對于開發高性能SmCo7型永磁材料具有重要的意義。
大量研究者通過實驗和計算的方法研究了添加元素對SmCo7相穩定性的影響,目前已有超過20種元素摻雜SmCo7的相關研究報道[6~12]指出,通過添加穩定化元素能夠保持SmCo7結構的穩定。摻雜元素基本可以分為3類:一是3d層電子未填滿的元素,例如Ti、Zr、Fe、Cu等;二是半導體元素,例如Si和Ge;三是4d層未填滿的元素,例如Ag、Mo、Nb等,以及5d層電子未填滿的元素,如Hf。不同元素摻雜對SmCo7合金的穩定性具有不同的影響,例如,過渡族元素Zr部分取代Co-Co啞鈴對可以使SmCo7具有穩定的TbCu7結構[3];Cr和Mo摻雜SmCo7時優先占據Co的2e晶位,這2種元素摻雜具有提高SmCo7相穩定性的效果[12];半導體元素Si摻雜也可提高SmCo7的穩定性[13];少量Hf摻雜SmCo7時可獲得穩定的單相,Hf優先占據Co的2e晶位,當溫度升高或摻雜量增加時,Hf開始占據Co的3g晶位,此時會引起SmCo7相失穩轉變[14];Al摻雜SmCo7會產生3種相,分別為SmCo7、Sm2Co17和未知相,不能使SmCo7的單相穩定存在[15]。Luo等[16]研究表明,包括Nb和V的15種添加元素中只有Si、Cu、Ti、Zr和Hf元素可以穩定SmCo7單相。而第一性原理計算確定了Zr添加可以使SmCo7的結構穩定,并且得出其占據Co的2e或3g晶位時合金結構最穩定[17]。
摻雜元素在影響SmCo7合金結構穩定性的同時,對磁性能也會產生影響。研究[13]表明,非磁性元素摻雜通常會導致磁矩與飽和磁化強度的降低,例如Si摻雜會削弱SmCo7的磁矩,并且隨著Si含量的增加SmCo7的晶胞體積增加,Curie溫度和最大磁能積都逐漸降低。Ga或Al取代部分Co時,SmCo7合金的飽和磁化強度和Curie溫度明顯降低[13,18]。元素取代對Co次晶格的磁矩影響較大[17],添加不同摻雜量的Mo時,SmCo7合金的飽和磁化強度隨摻雜元素含量的增加而減小[12]。Cr摻雜體系中,SmCo7-xCrx的矯頑力隨著Cr含量的增加顯著提高[12]。Cu添加會引起SmCo7合金晶格常數增大,隨著合金中Cu含量的增加,Curie溫度逐漸降低[19]。
綜上所述,采用元素摻雜的方法,可以使SmCo7相穩定存在。盡管已有關于不同種類元素摻雜對SmCo7合金結構穩定性和磁性能影響的大量研究,但是并未獲得共識,且所研究的元素種類仍然有限。Liu等[20]通過機器學習的方法預測Mn、Fe、In和Sn等元素的添加有益于維持Sm-Co合金的高飽和磁化強度,在Sm-Co體系磁性材料的成分設計時,摻雜這些元素不明顯降低飽和磁化強度,因此可在較大摻雜量條件下追求綜合磁性能指標的協同提升。例如,過渡族元素Mn和主族元素In有利于SmCo5體系的綜合性能[21],但是關于Mn和In添加到SmCo7合金中對體系穩定性和磁性能影響的研究卻鮮見報道。反鐵磁元素Mn摻雜可提高SmCo5體系總磁矩,而該元素在SmCo7體系中是否會產生同樣效果,值得進一步研究。實驗研究[21]得出,In元素摻雜SmCo7會產生SmCo5、Sm2Co17和SmCo7 3種物相,但In原子在混合相中如何影響基體穩定性及其微觀機理至今沒有明確認識。因此,以上問題需要借助第一性原理計算的方法,從幾何構型、電子結構等方面進行深入分析。然而,由于一直缺乏適合第一性原理計算的SmCo7的結構模型,限制了利用第一性原理計算進行相關的研究。
針對以上問題,本工作首先對目前存在的幾種用于第一性原理計算的SmCo7的近似模型進行總結分析,并通過深入研究TbCu7結構的特點,建立準確有效的適用于第一性原理計算的SmCo7結構模型。在此基礎上,結合前期SmCo5型合金中摻雜元素的篩選結果[20],建立Mn和In 2種元素單獨摻雜的SmCo7的模型,基于第一性原理密度泛函理論,計算摻雜體系的總能量、電子結構和磁矩等性質。利用形成能的計算研究摻雜元素對體系穩定性的影響,通過分析電子結構研究摻雜元素對體系穩定性及磁性能的影響規律,由此揭示添加元素對SmCo7結構穩定性和磁性能的作用機制。進一步結合統計熱力學分析方法,通過Maxwell-Boltzmann分布概率計算摻雜元素在SmCo7中占位概率隨溫度的變化,分析溫度對體系結構穩定性的影響。
Buschow[4]認為,TbCu7型結構是CaCu5型結構的衍生物,其中Ca位被2/9的Cu-Cu啞鈴對隨機取代。張昌文[22]建立了SmCo7-xTix的團簇結構Sm5Co28Ti6。Li等[19]建立了含有448個原子的SmCo7無序化的結構模型,但模型中的原子數量過于龐大,不適合第一性原理計算。Chen等[17]建立了含有25個原子的SmCo7.3的近似模型。張哲旭[23]通過實驗結果擬合晶格常數的方法建立了SmCo8.5的近似模型,其后華剛[24]在SmCo7超胞的基礎上進行簡化,得到了SmCo6.75的近似模型。以上幾種結構模型中存在的普遍問題是:SmCo7模型是在SmCo5超胞結構中由1個Co-Co啞鈴對替代1個Sm原子得到,導致多數模型的啞鈴對占比不準確,不能有效地反應SmCo7真實的結構及磁性;而符合SmCo7結構特點的無序計算模型中原子數量卻非常大,無法利用第一性原理進行計算。
針對這一矛盾問題,本工作基于Sm-Co基二元合金的晶體結構轉變規律分析,建立了Co-Co啞鈴對占比準確、單胞中原子數量適合第一性原理計算的SmCo7模型。建立SmCo7結構模型的傳統方法一般是在SmCo5單胞基礎上按(1 × 1 × 9)擴大9倍后,用2個Co-Co啞鈴對隨機替換2個Sm原子,得到SmCo7型結構,但問題是Co-Co啞鈴對的具體位置以及Co-Co原子間距不能確定,導致無法精確構建SmCo7晶體結構。通過Sm-Co二元合金中相結構轉變的研究,發現Sm2Co17 R型結構可由SmCo5轉變得到,其轉變過程是,SmCo5單胞按(1 × 3 × 3)擴大9倍后,再將得到的9倍SmCo5超胞中的3個Sm原子用3個Co-Co啞鈴對進行替代,則完成Sm9Co45到Sm6Co51的轉變。如圖1a所示,利用Materials Studio 軟件建立了Sm2Co17 R相的晶體結構模型。通過對比SmCo7和Sm2Co17中的各位點原子分布情況,發現利用Sm原子逆向替代Co-Co啞鈴對,則無需考慮Co-Co啞鈴對的Co原子間距及具體位置等問題。由此將Sm2Co17的3個Co-Co啞鈴對中的1個替換成Sm原子,即可得到SmCo7超胞。按照這種思路,構建了SmCo7的晶體結構,如圖1b所示。此結構在原子比例上恰好為Sm∶Co = 1∶7,同時具有SmCo5的結構特性和Co-Co啞鈴對的準確占比。在替換啞鈴對的選擇上,依據頭對頭不替換的原則,虛線圓圈位置的Co-Co啞鈴對替換為Sm,模型更為合理。
圖1 Sm2Co17 R相轉變為SmCo7的晶體結構示意圖
Fig.1 Schematics for the transition of crystal structure from Sm2Co17 R phase (a) to SmCo7 (b)
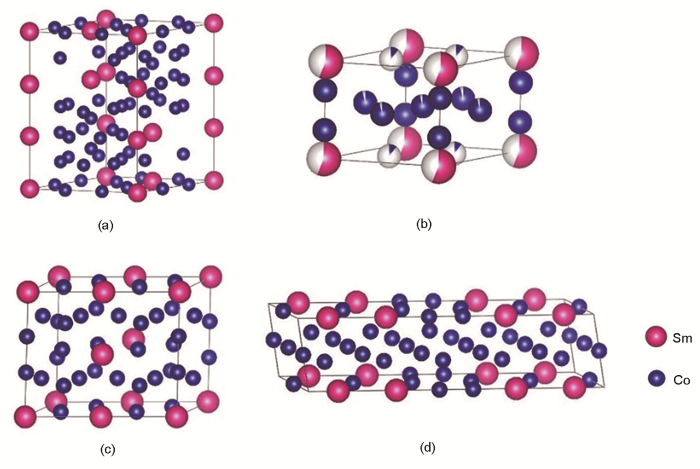
將建立的SmCo7模型與文獻[17,23,24]中已有的3種SmCo7近似模型進行對比,如圖2a~d所示。圖2a為本工作新建立的SmCo7模型,共56個原子,包含7個Sm原子,49個Co原子,其中18個Co原子占據2c晶位,4個Co原子占2e晶位,27個Co原子占3g晶位,2e晶位的Co-Co啞鈴對占比為2/9。圖2b為SmCo8.5模型[23],共38個原子,包含4個Sm原子和34個Co原子,其中2e晶位的Co原子有4個,2c晶位的Co原子有12個,3g晶位的Co有18個,Co-Co啞鈴對占比為2/6。圖2c為SmCo7.3模型[17],一共有25個原子,包含3個Sm原子和22個Co原子,其中2e位置的Co原子有2個,Co-Co啞鈴對占比為2/8。圖2d為SmCo6.75模型[24],共有31個原子,其中Sm原子有4個,Co的3g位置原子有15個,Co的2c位置原子有10個,Co的2e晶位的原子有2個,Co-Co啞鈴對占比為2/10。比較分析可見,只有SmCo7模型在原子比例上準確滿足Sm∶Co為1∶7,且保持本征的CaCu5結構特性,Co-Co啞鈴對占比準確。因此,本工作建立的模型確定為第一性原理計算SmCo7體系的最佳結構模型。
圖2 SmCo7超晶胞結構及與文獻[17,23,24]報道的SmCo7近似結構模型示意圖
Fig.2 Schematics of crystal structure models of SmCo7 supercell in present work (a), and SmCo8.5[17] (b), SmCo7.3[23] (c), and SmCo6.75[24] (d) supercells in Refs.[17,23,24]
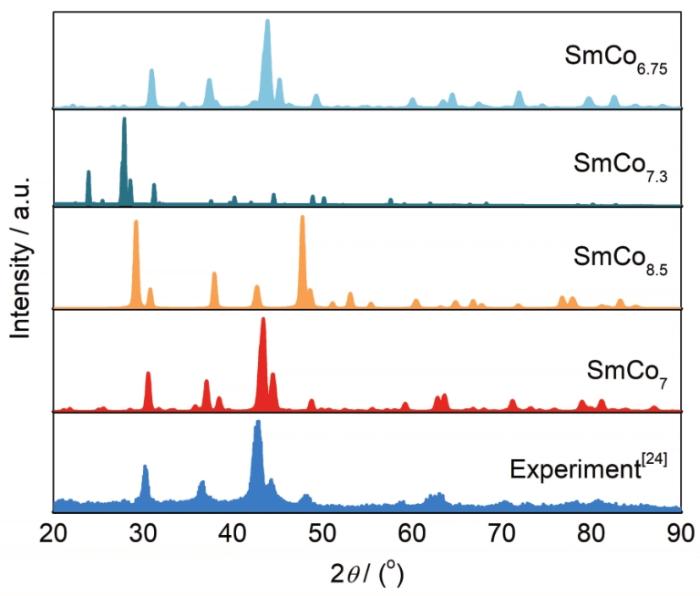
利用Materials Stuido中集成的Reflex模塊對1.1節中4種SmCo7結構模型進行物相衍射模擬分析,結果如圖3所示。SmCo8.5和SmCo7.3 2種結構模型的XRD峰值與實驗峰值[24]偏差很大,表明這2種結構難以代表SmCo7的真實結構特性。SmCo6.75和SmCo7結構模型的XRD譜與實驗結果[24]相近,僅在30°~40°之間存在1個雜相的峰。綜合分析可知,本工作采用2/9的Co-Co啞鈴對取代比例構建的結構模型與實驗結果吻合良好,證明了SmCo7結構模型建立的合理性。
圖3 4種SmCo7晶體結構模型對應的XRD模擬結果與實驗結果[24]的比較
Fig.3 Comparison for the simulated XRD peak positions among the four SmCo7 structure models and the experimental result[24]
本工作計算Mn和In 2種元素單摻雜的SmCo7體系,構建摻雜模型時采用1.1節中建立的SmCo7的7倍超胞為基體,折合SmCo7單胞的晶格常數為:a = b = 0.4888 nm,c = 0.4107 nm,c / a = 0.840。考慮Mn和In 2種元素在Co中的溶解度,將各模型中的摻雜元素M的濃度設為2% (原子分數,下同),同時考慮M原子可能優先占據Co原子的3種不同晶位。首先建立Mn摻雜的1組模型,分別為未摻雜SmCo7超胞,Mn分別占據2c、2e和3g晶位的結構模型。
根據本研究組在In摻雜SmCo7實驗方面的工作結果可知,In原子在Sm-Co體系中的作用比較復雜。尤其在亞穩相SmCo7基體中,當In原子添加濃度在1%~2%時,除主相SmCo7外,還存在SmCo5和Sm2Co17 2種雜相,當In的濃度超過2%,還會生成新的雜相Sm2Co9In3。在不考慮高摻雜量生成Sm2Co9In3的情況下,本工作研究In在Sm-Co混合相中的作用機制,分別建立In摻雜SmCo5、SmCo7和Sm2Co17超胞的一系列模型進行計算。為了方便對比分析,將SmCo5單胞擴大為9倍超胞,同時考慮In在3種Sm-Co基體可能占據不同位點的Co原子,建立一系列的模型。
本研究所有的計算都采用基于密度泛函理論的VASP軟件進行計算[25,26]。泛函形式采取GGA-PBE方法[27,28]。進行結構幾何優化時,平面波截斷能設置為450 eV,原子的自洽總能量差和收斂準則分別設為10-4 eV和0.1 eV/nm,選用K點設置為3 × 3 × 2。計算時各原子的電子組態分別為:Sm-5s25p66s2、Co-3d74s2、Mn-3d54s2、In-4d105s25p1。本研究中重點關注元素摻雜對SmCo7結構穩定性和磁矩的影響,而Sm-Co原子間的4f-3d相互作用主要影響Sm-Co體系的磁晶各向異性能大小,因此可將4f電子視為芯內電子處理,即選用Sm-3贗勢進行計算。
首先,對構建的SmCo7模型進行幾何結構優化,使建立的晶胞處于體系能量最穩定的狀態;隨后用Mn和In在不同位點替代Co原子,并對得到的晶胞按照相同的計算參數進行幾何結構優化,并在此優化基礎上,通過引入電子自旋,進一步完善結構優化。實驗研究得到的SmCo5晶格參數為a = b =0.4987 nm,c = 0.3981 nm,c / a = 0.798[29];計算得到的晶格參數為a = b = 0.4978 nm,c = 0.3951 nm,c / a = 0.793 (折合成SmCo5單胞)。SmCo7計算得到的晶格參數為a = b = 0.4863 nm,c = 0.4029 nm,c / a = 0.828,實驗值為a = b = 0.4936 nm,c = 0.4007 nm,c / a = 0.812[15]。如表1所示,計算得出的SmCo5和SmCo7的晶格參數與實驗值差異小于2%,說明建立的SmCo7模型合理,并且計算方法可靠。對比二元SmCo5和SmCo7單胞晶格參數發現,當引入Co-Co啞鈴對后,體系的a減小,c增大,c / a有所增加。
表1 SmCo5和SmCo7超胞幾何優化前后的晶格參數與實驗值[15,29]對比
Table 1
為研究體系的物相穩定性及元素摻雜的難易程度,計算了初始體系和摻雜SmCo6.8M0.2體系的形成能Eform,可描述為[30]:
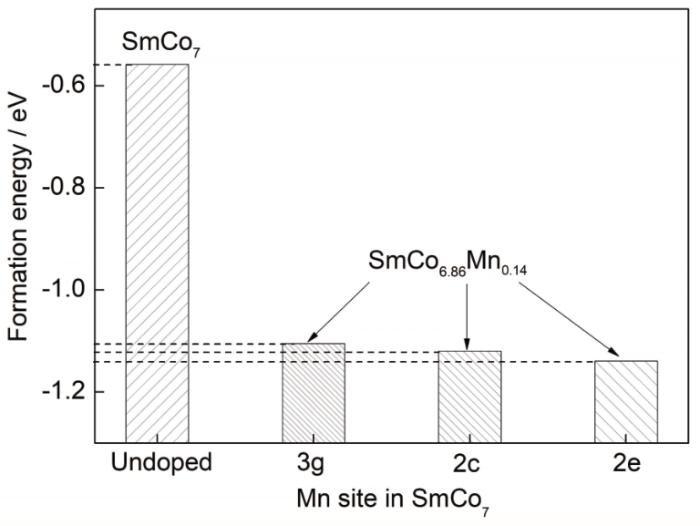
式中,E(total)為摻雜體系的總能量,n1、n2和n3分別為對應元素的原子個數,E(Sm)、E(Co)和E(M)分別是Sm、Co和M元胞的總能量。形成能為正值表示該元素摻雜較難,且體系物相穩定性較弱,反之,負值則表示元素較易于摻雜,且可增強體系的物相穩定性。對Mn元素摻雜前后的各體系形成能進行計算,結果如圖4所示。未摻雜的二元SmCo7合金的形成能為負值,但趨近于0,說明其結構穩定性不高。Mn元素的引入降低了亞穩相SmCo7合金的形成能,使SmCo7的穩定性有所增加。對比Mn取代不同晶位Co原子的SmCo6.86Mn0.14體系形成能,可知Mn在SmCo7基體中優先占位排序為:優先占據2e晶位,其次為2c晶位,最后為3g晶位。由于Mn占據3種不同晶位時的形成能差值較小,Mn元素的添加超過一定量時,易發生占位的轉變。
圖4 摻雜元素Mn在SmCo7體系中3g、2c和2e晶位的形成能計算結果
Fig.4 Calculated formation energies of doping element Mn at 3g, 2c, and 2e sites in SmCo7 and that of undoped alloy for comparison
根據2.2.1節分析得知,同一種摻雜元素在替代不同晶位上的Co原子時,體系的形成能存在一定的差值,說明摻雜元素的占位會對形成能產生影響。因此當摻雜元素的占位發生改變時,合金體系的晶體結構穩定性也會受到影響。這主要是由于SmCo7晶胞中的次晶格Co的3種占位具有不同的空間體積,同時處在不同的成鍵環境中。一般情況下,第一性原理計算的能量值是在0 K (-273℃)條件下獲得的,而晶體中的體積、原子半徑等因素,在實際中會受到溫度的影響。當溫度改變時,由于原子熱振動及晶體內點陣缺陷平衡濃度發生變化,會使原子間的距離發生改變,這不但會引起原子半徑的改變,還會改變不同占位下的空間環境,進而影響占據不同位點的概率以及體系的穩定性。因此,有必要研究溫度變化對摻雜元素占位產生的影響,以進一步分析溫度對體系形成能和穩定性的影響。考慮到SmCo7合金的適用溫度,利用Maxwell-Boltzmann分布定律[31],在0~900℃范圍內對其摻雜元素的占位概率(Pi)進行研究。
式中,gi為簡并度,i為晶胞中不同占位下的組態,ΔGi、ΔHi和ΔSi分別為Gibbs自由能、焓與熵的變化,Ef為通過第一性原理計算得到的形成能,P為壓力,ΔV為晶胞體積變化,T為溫度,kB為Boltzmann常數。熵變包括組態熵與振動熵2部分,每個原子的振動熵平均為0.1kB~0.2kB,組態熵(S)取決于置換晶位的數目和摻雜量的大小[32,33],可描述為[34]:
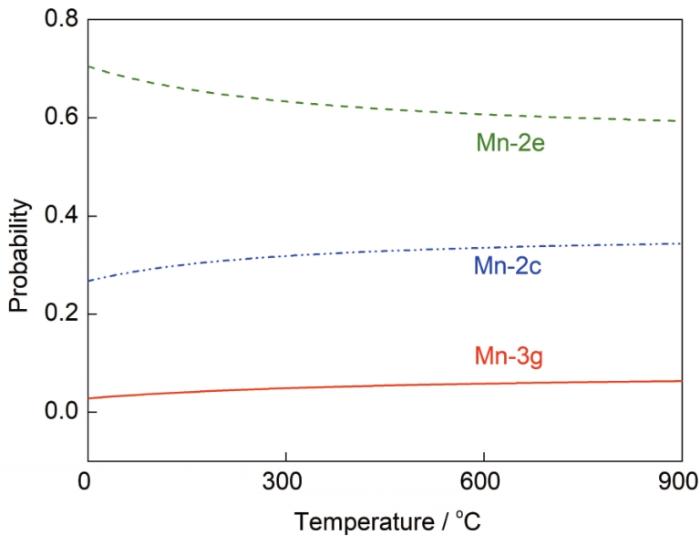
式中,Ω為組態數。由于摻雜元素引起的體積變化很小,因此采用近似處理PΔV = 0[35]。所以利用第一性原理計算得到的形成能,結合統計熱力學Maxwell-Boltzmann分布,即可預測SmCo6.86Mn0.14體系在較高溫度下的結構穩定性。在較寬的溫度范圍(0~900℃)內,SmCo7合金中Mn的摻雜位點占位概率隨溫度的變化關系如圖5所示。Mn占據Co-2e晶位的概率始終相對最高,其次是Co-2c晶位,占據3g晶位的概率趨近于0。從Maxwell-Boltzmann方程來看,影響概率的主要因素是體系能量,由于2e 晶位的取代能遠小于另外2種晶位,因此2e晶位的占位概率和穩定性最高。隨著溫度的升高,Mn占據Co-3g晶位的概率未發生明顯改變,說明Mn占據此晶位的概率始終較低。而2e晶位的占位概率緩慢降低,2c晶位的占位概率隨溫度逐漸升高。圖5的結果表明,Mn在SmCo7中的占位概率受溫度影響不顯著,Mn摻雜適用的溫度范圍較廣。
圖5 SmCo6.86Mn0.14體系中Mn在不同位點的占位概率隨溫度的變化
Fig.5 The calculated site occupation probability of Mn as a function of temperature for SmCo6.86Mn0.14
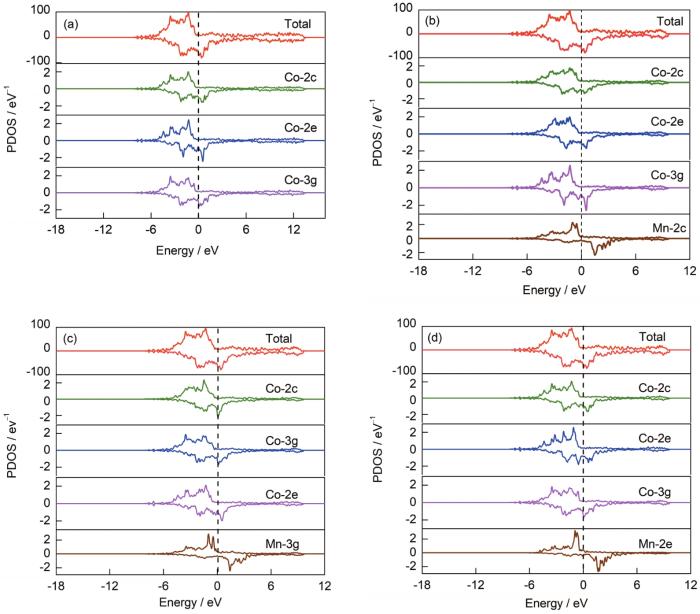
為闡明Mn添加對SmCo6.86Mn0.14體系穩定性影響的微觀機理,對Mn摻雜前后體系的偏態密度進行了計算,以此分析元素摻雜對體系電子結構的影響。體系的總態密度、Mn原子和不同位點的Co原子的偏態密度如圖6所示。
圖6 Mn摻雜前后各體系的總態密度(DOS)及各原子的偏態密度(PDOS)
(a) SmCo7 (b) SmCo6.86Mn0.14 (2c)
(c) SmCo6.86Mn0.14 (3g) (d) SmCo6.86Mn0.14 (2e)
Fig.6 Total density of states (DOSs) and partial density of states (PDOSs) of elements in undoped and Mn doped systems
對比Mn摻雜前后各體系總態密度圖可知,添加Mn后體系總態密度峰值降低,這是由于Mn的電子數目比Co少,使態密度峰值降低,離域性增強,說明體系的穩定性升高。如圖6b~d所示,在Fermi能級附近,Mn自旋向上峰值與不同位點的Co均具有峰型共振的現象,說明Mn與Co之間具有較強的相互作用。Mn占據不同位點時,其周圍Co原子偏態密度峰值明顯不同,當Mn占據2c位時,Co-3g偏態密度峰值明顯增高,Co-2c和Co-2e偏態密度峰值降低;當Mn占據3g位時,Co-2c偏態密度峰值略微增高,Co-3g和Co-2e偏態密度峰值下降;當Mn占據2e位時,周圍的Co-2c和Co-3g偏態密度變化較小,而Co-2e偏態密度在摻雜前后變化最為明顯,說明Mn-Co(2e)間相互作用最強,在增強體系穩定性的過程中起到主要作用,這與對體系形成能計算得到的Mn優先占據Co-2e晶位的結果相一致。
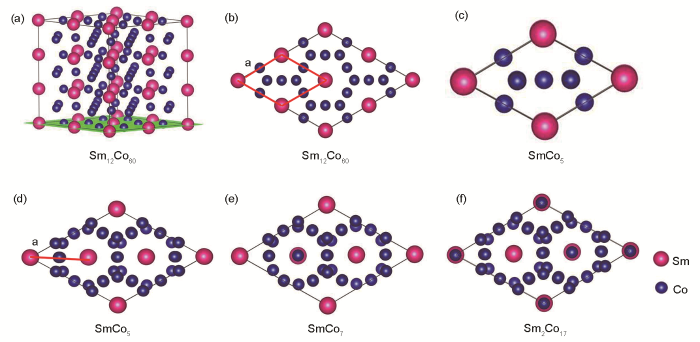
實驗表明In元素摻雜亞穩相SmCo7會產生SmCo5、SmCo7和Sm2Co17 3相共存的混合物。由于計算得到的晶胞參數屬于超胞體系,3種物相的超胞大小不同,因此要研究In添加對SmCo5、SmCo7和Sm2Co17晶胞變化的影響,需要將3種超胞折合成SmCo5單胞大小。如圖7所示,圖7a是12倍SmCo5 (1 × 3 × 4)的超胞結構圖,圖7b和c分別是12倍的SmCo5超胞和SmCo5單胞在(001)面的投影圖。圖7d是由Sm2Co17中的3個Co-Co啞鈴對全部替換成Sm原子后形成的9倍SmCo5體系。如圖7d~f所示,通過各結構模型在(001)面的投影分析,可以看出12倍SmCo5 (1 × 3 × 4)的超胞旋轉60°后可得到與SmCo5、SmCo7和Sm2Co17 3種結構相似的原子排布。在12倍SmCo5 (1 × 3 × 4)的超胞中折合成單胞的晶格常數a為紅色線段部分,即為計算得到的a和晶格常數b的1/4、晶格常數c的1/3,此時獲得的晶格常數與SmCo5單胞的相同。
圖7 Sm12Co60超晶胞結構及SmCo5、SmCo7和Sm2Co17模型在(001)平面投影示意圖
(a) Sm12Co60 supercell supercell structure
(b) Sm12Co60 supercell supercell (Supercell structure model projected on the (001) plane)(c) SmCo5 unit cell (d) SmCo5 supercell
(e) SmCo7 supercell (f) Sm2Co17 supercell
Fig.7 Diagram of Sm12Co60 supercell structureand the models of SmCo5, SmCo7, and Sm2Co17 projected on the (001) plane
考慮In在SmCo5中有2種可能占位,在SmCo7中有3種可能占位,在Sm2Co17中有4種可能占位,同時建立不同占位的結構模型,加上未摻雜模型共計12個模型,如表2所示,A、B和C分別為優化后的SmCo5、SmCo7和Sm2Co17模型,不同數字代表摻雜元素占據不同位點。對比未摻雜的3個模型的體積,可以看出,SmCo5的體積最大,Sm2Co17最小,這是由于Sm原子半徑較大,Sm被Co-Co啞鈴對替換后,引起體積收縮。由于In原子半徑較大,3類模型的體積均隨In的摻入而增大,使得摻雜體系的晶胞發生畸變,進而影響體系的穩定性。
表2 計算的In摻雜SmCo5、SmCo7和Sm2Co17前后的晶格參數和晶胞體積
Table 2
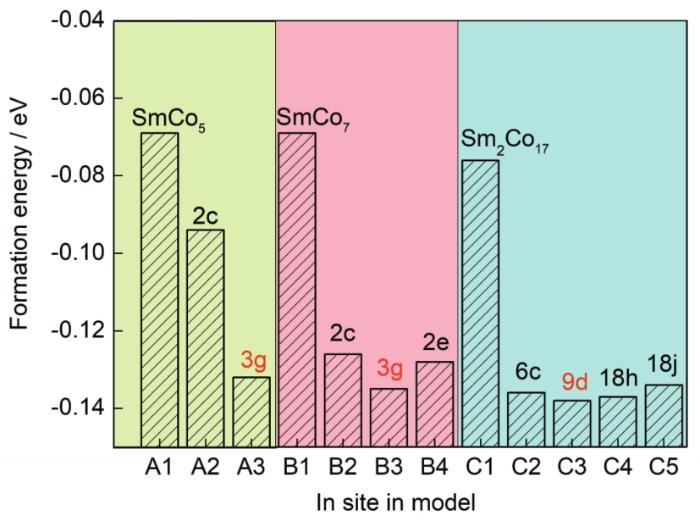
為了研究In的擇優占位規律,對摻雜前后的各體系形成能進行了計算,結果如圖8所示。Al、B1和C1代表未摻雜體系,其形成能均為負值,但都趨近于0,說明3種基體穩定性較低,易發生相分解,其中Sm2Co17形成能最低,SmCo7最高,這與SmCo7是亞穩相的實驗事實相符。比較In摻雜各體系的形成能,可知In在SmCo5基體中,優先占據3g晶位,在SmCo7中優先占據3g晶位,而在Sm2Co17中,優先占據9d晶位。當3種相共存時,In更傾向于優先進入Sm2Co17相中。
圖8 In摻雜的SmCo5、SmCo7和Sm2Co17體系中In原子占據不同晶位的形成能計算結果
Fig.8 Calculated formation energies of SmCo5, SmCo7, and Sm2Co17 systems with doped In at different sites and those of undoped systems for comparison
為進一步考察In摻雜Sm-Co體系在不同溫度下的占位概率變化特點,利用第一性原理計算得到的形成能,結合統計熱力學Maxwell-Boltzmann分布進行計算,結果如圖9所示。圖9a是In在SmCo5體系中Co的2c和3g晶位上的占位概率與溫度之間的關系。從圖中可以看到,In優先占據3g晶位,隨著溫度的升高,2種晶位的占位概率發生改變,3g晶位的占位概率略有下降,同時占據2c晶位的概率稍有增加。當占據不同位點的形成能差值較小時,位點的幾何環境相似,摻雜元素易發生占位的轉變。如圖9b所示,隨著溫度的升高,In占據3g位點概率降低,占據2e位點的概率增大,占據2個不同位點的概率具有相交的趨勢。在Sm2Co17中也具有相似的規律,如圖9c所示,隨著溫度的升高,In在9d晶位的占位概率出現明顯下降趨勢,而其他3種占位的概率則同時出現升高的現象。對比In在3種體系中的占位概率隨溫度的變化規律可知,在SmCo5中In不容易發生占位轉變,這與圖8所示的在SmCo5中占據不同位點的形成能差值較大相吻合。而在SmCo7中In最易發生占位的轉變,這也表明,SmCo7基摻雜體系的結構穩定性受溫度影響較大。
圖9 摻雜元素In在不同體系中的占位概率隨溫度的變化
(a) SmCo5 (b) SmCo7 (c) Sm2Co17
Fig.9 Variations of occupation probability of In doping with temperature in different systems
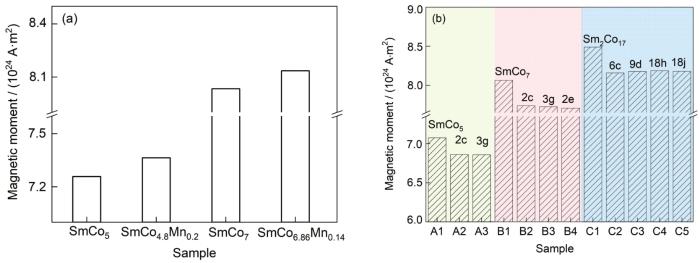
摻雜Mn前后SmCo5和SmCo7體系的磁矩變化如圖10a所示。在SmCo7體系中摻雜Mn元素,體系總磁矩出現升高的現象,與文獻[21]中添加Mn可使SmCo5體系總磁矩升高的結論一致,說明Mn元素有利于提高Sm-Co體系合金的飽和磁化強度。在SmCo5和SmCo7超胞中分別添加1個Mn原子后,總磁矩增加的大小相似,Mn的原子磁矩大小對體系總磁矩影響明顯。
圖10 摻雜Mn和In前后的SmCo5、SmCo7 和Sm2Co17超胞總磁矩
(a) SmCo5 and SmCo7 supercells with or without Mn doping
(b) SmCo5, SmCo7, and Sm2Co17 supercells with or without In doping at different sites
Fig.10 Total magnetic moments of SmCo5, SmCo7, and Sm2Co17 systems doped Mn and In at different sites and undoped systems
對In摻雜SmCo5、SmCo7和Sm2Co17體系不同占位的各結構模型的總磁矩進行計算,結果如圖10b所示。在未摻雜體系中總磁矩由大到小的順序為Sm2Co17 > SmCo7 > SmCo5,這是由于Sm-Co體系磁性主要來源于Co次晶格,體系中Co原子占比越大,體系總磁矩越大,因此Sm2Co17合金的飽和磁化強度最高。隨著In元素的引入,SmCo5、SmCo7和Sm2Co17體系的總磁矩均有所降低,一方面是因為非磁性元素In替代磁性元素Co會造成一部分磁矩的損失;另一方面,In會影響其周圍Co原子的磁矩,使其被削弱。但由于In原子半徑較大,使周圍Co-Co原子間距減小,從而提高部分次近鄰處Co原子的磁矩,對總磁矩的減小起到補償作用。因此相比于絕大多數元素添加后均明顯降低Sm-Co體系的飽和磁化強度而言,In的添加對于Sm-Co體系的飽和磁化強度降低程度較小,In可以被認為是對Sm-Co體系飽和磁化強度的友好型摻雜元素。
(1) 通過分析Sm-Co基二元合金結構轉變規律,采用Sm2Co17相中的Co-Co啞鈴對逆向替換Sm的方法,成功構建了Sm∶Co原子比例恰好為1∶7的晶體結構模型,突破了長久以來沒有精準Co-Co啞鈴對占比且適用于第一性原理計算的SmCo7結構模型的難題,并通過計算驗證了模型的合理性。
(2) 摻雜濃度為2% (原子分數)的Mn元素可降低SmCo7亞穩相的形成能,提升SmCo7的穩定性;對于不同溫度下占位概率的計算表明,Mn的占位概率隨溫度升高變化不明顯,因此摻雜Mn可在較寬溫度范圍內使用;電子結構分析可知,Mn-Co間存在較強的相互作用,有利于提升體系的穩定性。
(3) 添加濃度為2%的In,SmCo7體系中存在SmCo5、SmCo7和Sm2Co17 3種相,In優先占據Sm2Co17的9d晶位。添加少量In可使Sm-Co體系的形成能降低,從而提高SmCo5、SmCo7 和Sm2Co17相的結構穩定性。
(4) 添加反鐵磁元素Mn有利于提高SmCo7體系的總磁矩,促使飽和磁化強度升高;而添加元素In使SmCo5、SmCo7和Sm2Co17體系總磁矩均降低,但是降低程度較小。添加相同原子個數的In引起不同Sm-Co體系的凈磁矩減小程度相似。
1 模型構建與計算方法
1.1 模型構建
圖1
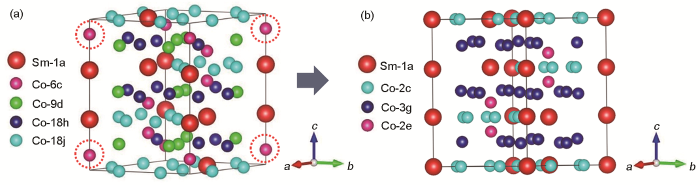
圖2
1.2 模型合理性驗證
圖3
1.3 摻雜模型建立
1.4 計算方法
2 計算結果分析
2.1 SmCo7計算結果分析
Model
Lattice parameter / nm
c / a
a
b
c
SmCo5
0.4978
0.4978
0.3951
0.793
Experiment[29]
0.4987
0.4987
0.3981
0.798
SmCo7
0.4863
0.4863
0.4029
0.828
Experiment[15]
0.4936
0.4936
0.4007
0.812
2.2 Mn摻雜對SmCo7穩定性的影響
2.2.1 穩定性及擇優占位
圖4
2.2.2 溫度對擇優占位的影響
圖5
2.2.3 電子結構分析
圖6
2.3 In摻雜對SmCo7結構穩定性的影響
2.3.1 穩定性及擇優占位
圖7
Number
Model
a / nm
c / nm
c / a
V / nm3
A1
SmCo5 (9 supercell)
0.4968
0.3943
0.790
0.759
A2
Sm9Co44In (2c)
0.4900
0.3962
0.808
0.772
A3
Sm9Co44In (3g)
0.4928
0.3958
0.803
0.773
B1
SmCo7
0.4863
0.4029
0.828
0.741
B2
Sm7Co48In (2c)
0.4224
0.4054
0.959
0.754
B3
Sm7Co48In (3g)
0.4226
0.4039
0.956
0.754
B4
Sm7Co48In (2e)
0.4233
0.4038
0.954
0.752
C1
Sm2Co17
0.4821
0.4046
0.840
0.731
C2
Sm6Co50In (6c)
0.4195
0.4063
0.968
0.743
C3
Sm6Co50In (9d)
0.4198
0.4062
0.967
0.745
C4
Sm6Co50In (18h)
0.4199
0.4062
0.967
0.745
C5
Sm6Co50In (18j)
0.4196
0.4075
0.971
0.745
圖8
2.3.2 溫度對In摻雜擇優占位的影響
圖9

2.4 Mn和In單摻雜對SmCo7磁矩的影響
圖10
3 結論
來源--金屬學報







 滬公網安備31011202020290號
滬公網安備31011202020290號
